Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tứ giác BCB'C' có
\(\widehat{BC'C}=\widehat{BB'C}\left(=90^0\right)\)
\(\widehat{BC'C}\) và \(\widehat{BB'C}\) là hai góc cùng nhìn cạnh BC
Do đó: BCB'C' là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)


1.Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm

a: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Xét (O) có
ΔABA' là tam giác nội tiếp
AA' là đường kính
Do đó: ΔABA' vuông tại B
=>BA'\(\perp\)AB
mà CH\(\perp\)AB
nên BA'//CH
Xét (O) có
ΔACA' là tam giác nội tiếp
AA' là đường kính
Do đó: ΔACA' vuông tại C
=>AC vuông góc CA'
mà BH vuông góc AC
nên BH//A'C
Xét tứ giác BHCA' có
BH//CA'
BA'//CH
Do đó: BHCA' là hình bình hành

Ta có: = 2
= 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và =
(đối đỉnh)
mà = 180o -
= 180o - 60o = 120o
nên = 120o (2)
=
+
= 60o + = 60o+ 60o
(sử dụng góc ngoài của tam giác)
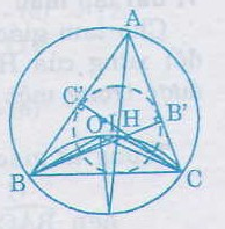
Do đó = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn
Ta có: \(\widehat{BOC}\) = 2\(\widehat{BAC}\) = 2.60o = 120o (1)
(góc nội tiếp và góc ở tâm cùng chắn một cung)
và \(\widehat{BHC}\) = \(\widehat{B'HC'}\) (đối đỉnh)
mà \(\widehat{B'HC'}\) = 180o - \(\widehat{A}\) = 180o - 60o = 120o
nên \(\widehat{BHC}\) = 120o (2)
\(\widehat{BIC}\) = \(\widehat{A}\) + \(\dfrac{\widehat{B}+\widehat{C}}{2}\)
= 60o + \(\dfrac{180^0-60^0}{2}\) = 60o+ 60o
(sử dụng góc ngoài của tam giác)

Do đó \(\widehat{BIC}\) = 120o
Từ (1), (2), (3) ta thấy các điểm O, H, I cùng nằm trên các cung chứa góc 120o dựng trên đoạn thẳng BC. Nói cách khác, năm điểm B, C, O, H, I cùng thuộc một đường tròn