Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Answer:
A C B D E
a. Tam giác ABC cân tại A
=> Góc ABC = góc ACB
=> BD là tia phân giác của góc ABC
\(\Rightarrow\widehat{BDC}=\frac{\widehat{ABC}}{2}\)
CE là tia phân giác của góc ACB
\(\Rightarrow\widehat{BCE}=\frac{\widehat{ACB}}{2}\)
=> Góc BDC = góc BCE
Xét tam giác BCE và tam giác CBD:
BC cạnh chung
Góc CBE = góc BCD
Góc BCE = góc CBD
=> Tam giác BCE = tam giác CBD (g.c.g)
=> BD = CE
b. Có: \(\frac{BE}{AB}=\frac{DC}{AC}\Rightarrow ED//BC\)
c. Có: \(\frac{AD}{DC}=\frac{AB}{BC}\)
\(\Rightarrow\frac{AD}{DC}=\frac{6}{4}=\frac{3}{2}\)
\(\Rightarrow AD=\frac{3}{2}DC\)
Mà AD + DC = AC
\(\frac{3}{2}DC+DC=6\)
\(\Rightarrow DC=2,4cm\)
\(\Rightarrow AD=3,6cm\)
Có \(\frac{ED}{BC}=\frac{AD}{AC}\)
\(\Rightarrow ED=\frac{BC.AD}{AC}=\frac{4.3,6}{6}=2,4cm\)

a b c d e 1 1 6 6 4
câu a
tam giác abc có ab = ac
=> tam giác abc cân tại a
=> góc b = góc c
=> góc b1 = góc c1 (phân giác 2 góc = nhau)
tam giácc bcd và tam giác cbe có
chung bc
góc b = góc c
góc b1 = góc c1
=> tam giác bcd = tam giác cbe (gcg)
=> bd = ce
câu b
câu a
\(\)=> cd = be
có ab = ac
\(=>\dfrac{cd}{ac}=\dfrac{be}{ab}\\ \)
=> ed // bc (ta lét đảo)
câu c
tam giác abc có bd là phân giác góc b
\(=>\dfrac{ab}{bc}=\dfrac{ad}{cd}\\ =>\dfrac{ab}{bc+ab}=\dfrac{ad}{ad+cd}\\ =>\dfrac{ab}{bc+ab}=\dfrac{ad}{ac}\\ =>\dfrac{6}{6+4}=\dfrac{ad}{6}\\ =>\dfrac{6}{10}=\dfrac{ad}{6}\\ =>ad=3,6\left(cm\right)\)
có ad +cd = ac
=> 3,6 + cd = 6
=> cd = 2,4 (cm)
có ed // bc
\(=>\dfrac{ed}{bc}=\dfrac{ad}{ac}\\ =>\dfrac{ed}{4}=\dfrac{3,6}{6}\\ =>ed=2,4\left(cm\right)\)
thế thoi, chúc may mắn :)

a) Xét tam giác BEC và tam giác CDB có:
góc ABC = góc ACB (tam giác ABC cân tại A);
BC chung;
góc ECB = góc DBC \(\left(=\dfrac{\widehat{ABC}}{2}=\dfrac{\widehat{ACB}}{2}\right)\)
=> tam giác BEC = tam giác CDB (g-c-g)
=> EC = DB (2 cạnh tương ứng)
b) theo câu a) ta có tam giác EBC = tam giác DCB (g-c-g)
=> BE = DC (2 cạnh tương ứng)
=> AE = AD (=AB-BE=AC-DC)
=> tam giác AED cân tại A
=> góc AED = (1800 - góc BAC):2 (*)
cũng như trong tam giác ABC cân tại A thì
góc ABC = (1800 - góc BAC):2 (**)
Từ (*)(**)=> góc AED = góc ABC (ở vị trí đồng vị)
=> ED song song với BC
c) Theo tính chất đường phân giác trong tam giác thì ta có:
\(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Leftrightarrow\dfrac{AB}{AD}=\dfrac{BC}{DC}\Leftrightarrow\dfrac{AB+BC}{AD+DC}\)
\(\Leftrightarrow\dfrac{AB+BC}{AC}=\dfrac{6+4}{6}=\dfrac{10}{6}=\dfrac{5}{3}\)
\(\Rightarrow AD=AB:\dfrac{5}{3}=6:\dfrac{5}{3}=\dfrac{18}{5}=3,6\left(cm\right)\)
và \(DC=AC-AD=6-3,6=2,4\left(cm\right)\)
Mặt khác:\(\dfrac{AD}{AC}=\dfrac{ED}{BC}\Rightarrow ED=\dfrac{AD.BC}{AC}=\dfrac{3,6.4}{6}=2,4\left(cm\right)\)

áp dụng tính chất đường phân giác ta có : AD/DC=AB/BC hay AD/AB=DC/BC
theo tính chất của dãy tỉ số bằng nhau, ta co: AD/AB=DC/BC =( AD+DC)/ (AB+BC)=6/10=3/5
VẬY AD = 3/5 x AB=3/5 x 6 =18/5 cm
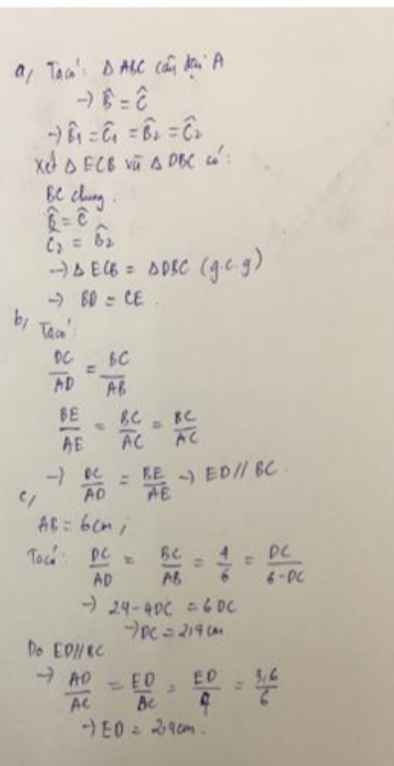

cc giúp mk nha
<3
A B C E D