BB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BB
1
YV
16 tháng 2 2019
xét hai tam giác ABM và tam giác ACM có
AB<AC (gt)
AC cạnh chung
góc BAM < góc CAM
suy ra tam giác ABM < tam giác ACM
suy ra MB <MC ( 2 cạnh tương ứng)
6 tháng 3 2023
a:AB<AC
=>góc C<góc B
góc BAM+góc B+góc AMB=góc CAM+góc C+góc AMC
mà góc BAM=góc CAM; góc B>góc C
nên góc AMB<góc AMC
b: Xét ΔABC có AM là phân giác
nên MB/AB=MC/AC
mà AB<AC
nên MB<MC
c: góc AMB<góc AMC
=>góc AMB<1/2(góc AMB+góc AMC)=90 độ
=>góc AMB nhọn
LA
9 tháng 4 2017
CMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMH
NT
0
9 tháng 5 2016
Trên AB lấy D sao cho AD=AC =>AB-AC=BD(1)
Nối M và D
Xét tam giác AMC và AMD
góc CAM=MAD
AM chung AC=AD
=>Tam giác AMC=AMD
=>CM=MD(......)(2)
Xét tam giác MDB
MB-MD<DB( BĐT tam giác)(3)
Thay1;2 vào 3
Ta được MB-MC< AB-AC
BK
15 tháng 6 2021
Trên cạnh AB lấy điểm E sao cho AE=AC
Xét tam giác ACM và tam giác AEM có:
AM chung
góc CAM=góc EAM(AM là tia p/g của góc A)
AC=AE(cách vẽ)
=>tam giác ACM và tam giác AEM(c-g-c)
=>CM=EM(2 cạnh tương ứng)
Xét tam giác NEB có:MB-ME<EB(BĐT tam giác)
Mà MC=ME(cmt)
=>MB-MC<EB (1)
Ta có:AC=AE(cách vẽ)
Mà AB-AE=EB
=>AB-AC=EB (2)
Từ (1) và (2) =>MB-MC<AB-AC
Hay |MB-MC|<AB-AC (đpcm)
28 tháng 6 2020
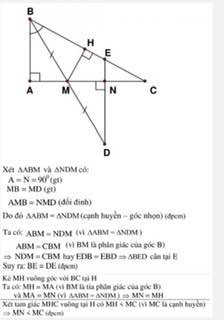
A B C M N H E D I I
Xét \(\Delta ABM\)và \(\Delta NDM\)có: \(\hept{\begin{cases}\widehat{A}=\widehat{DNM}=90^o\left(gt\right)\\MB=MD\left(gt\right)\\\widehat{AMB}=\widehat{NMD}\end{cases}}\Rightarrow\Delta ABM=\Delta NDM\left(ch-gn\right)\left(đpcm\right)\)
Ta có \(\widehat{ABM}=\widehat{NDM}\left(\Delta ABM=\Delta NDM\right)\)
\(\widehat{ABM}=\widehat{CBM}\)(BM là phân giác \(\widehat{B}\))
\(\Rightarrow\widehat{NDM}=\widehat{CBM}\)hay \(\widehat{EDB}=\widehat{EBD}\)
\(\Rightarrow\Delta BED\)cân tại E
=> BE=DE (đpcm)
Kẻ MH vuông góc với BC tại H
Ta có MH=MA (vì BM là tia phân giác của \(\widehat{B}\))
và MA=MN (\(\Delta ABM=\Delta NDM\))
=> MN=MH
Xét \(\Delta MHC\)vuông tại H có MH<MC (vì MC là cạnh huyền)
=> MN<MC (đpcm)
