Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
Do đó: ΔBAM=ΔBDM(cạnh huyền-góc nhọn)
Suy ra: BA=BD(hai cạnh tương ứng)
Xét ΔABD có BA=BD(cmt)
nên ΔABD cân tại B(Định nghĩa tam giác cân)
b) Ta có: ΔBAM=ΔBDM(cmt)
nên MA=MD(hai cạnh tương ứng)
Ta có: BA=BD(cmt)
nên B nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MA=MD(cmt)
nên M nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD(Đpcm)
c) Xét ΔAME vuông tại A và ΔDMC vuông tại D có
MA=MD(cmt)
\(\widehat{AME}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔAME=ΔDMC(cạnh góc vuông-góc nhọn kề)
Suy ra: ME=MC(hai cạnh tương ứng)
Xét ΔMEC có ME=MC(cmt)
nên ΔMEC cân tại M(Định nghĩa tam giác cân)
d) Ta có: ΔAME=ΔDMC(cmt)
nên AE=DC(hai cạnh tương ứng)
Ta có: BA+AE=BE(A nằm giữa B và E)
BD+DC=BC(D nằm giữa B và C)
mà BA=BD(cmt)
và AE=DC(cmt)
nên BE=BC
Xét ΔBEC có BE=BC(cmt)
nên ΔBEC cân tại B(Định nghĩa tam giác cân)
hay \(\widehat{BEC}=\dfrac{180^0-\widehat{EBC}}{2}\)(Số đo của một góc ở đáy trong ΔBEC cân tại B)(3)
Ta có: ΔBAD cân tại B(cmt)
\(\Leftrightarrow\widehat{BAD}=\dfrac{180^0-\widehat{ABD}}{2}\)(Số đo của một góc ở đáy trong ΔBDA cân tại B)
hay \(\widehat{BAD}=\dfrac{180^0-\widehat{EBC}}{2}\)(4)
Từ (3) và (4) suy ra \(\widehat{BAD}=\widehat{BEC}\)
mà \(\widehat{BAD}\) và \(\widehat{BEC}\) là hai góc ở vị trí đồng vị
nên AD//EC(Dấu hiệu nhận biết hai đường thẳng song song)

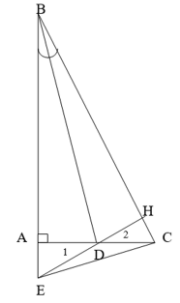
a). Xét t/g : ABD và HBD có:
góc A = góc H = 90\(^o\)
BD cạnh chung
góc ABD = góc HBD ( BD là tia ph/giác góc B)
do đó :
t/g ABD = t/g HBD ( cạnh huyền - góc nhọn).
b, Vì t/g ABD = t/g HBD
=> AD = HD và AB=HB (1) ( 2 cạnh tương ứng).
Xét t/g ADE và HDC có:
góc A = góc H = 90\(^o\)
góc D1 = góc D2 ( đối đỉnh).
AD = HD ( cmt)
do đó : t/g ADE = t/g HDC ( cạnh góc vuông - góc nhọn kề nó).
=> AE = HC ( 2) ( 2 cạnh tương ứng).
Từ (1) và (2) suy ra : AB + AE = HB + HC
Hay BE = BC
=> T/g BEC cân tại B.
c).
Theo cmt ta có AD = DH
Xét t/g vuông DHC vuông tại H có:
DH<DC
Do đó:
AD < DC

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
Suy ra: BA=BD
Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
mà \(\widehat{ABD}=60^0\)
nên ΔBAD đều
b: Ta có: ΔBAM=ΔBDM
nên MA=MD
Ta có: BA=BD
nên B nằm trên đường trung trực của AD\(\left(1\right)\)
Ta có: MA=MD
nên M nằm trên đường trung trực của AD\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BM là đường trung trực của AD
c: Xét ΔAME vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMC}\)
Suy ra: ΔAME=ΔDMC
Suy ra: ME=MC
hay ΔMEC cân tại M