Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay \(BC=\sqrt{100}=10cm\)
Xét ΔABC có AH là đường cao ứng với cạnh BC nên
\(S_{ABC}=\dfrac{AH\cdot BC}{2}\)(1)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}\)(2)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay \(AH=\dfrac{48}{10}=4.8cm\)
Vậy: AH=4,8cm
b) Xét tứ giác AEHF có
\(\widehat{EAF}=90^0\)(ΔABC vuông tại A, E∈AB, F∈AC)
\(\widehat{AEH}=90^0\)(HE⊥AB)
\(\widehat{AFH}=90^0\)(HF⊥AC)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
⇒AH=EF(Hai đường chéo của hình chữ nhật AEHF)
mà AH=4,8cm(cmt)
nên EF=4,8cm
Vậy: EF=4,8cm

a) Xét ΔABC có
F là trung điểm của AC(gt)
M là trung điểm của BC(gt)
Do đó: FM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒FM//AB và \(FM=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà E∈AB và \(AE=\dfrac{AB}{2}\)(E là trung điểm của AB)
nên FM//AE và FM=AE
Xét tứ giác AEMF có
FM//AE(cmt)
FM=AE(cmt)
Do đó: AEMF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEMF có \(\widehat{FAE}=90^0\)(ΔABC vuông tại A)
nên AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

Bài 1:
a: BC=17cm
AH=120/7(cm)
b: Xét tứ giác AMHN có góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
Suy ra: AH=MN=120/7(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nen \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a: Xét tứ giác AHBK có
M là trung điểm của AB
M là trung điểm của HK
Do đó: AHBK là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBK là hình chữ nhật
b:
Xét tứ giác AKHC có
AK//HC
AK=HC
Do đó: AKHC là hình bình hành
c: Xét ΔABC có
N là trung điểm của AC
H là trung điểm của BC
Do đó: NH là đường trung bình
=>NH//AB và NH=AB/2
hay NH//AM và NH=AM
=>AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi

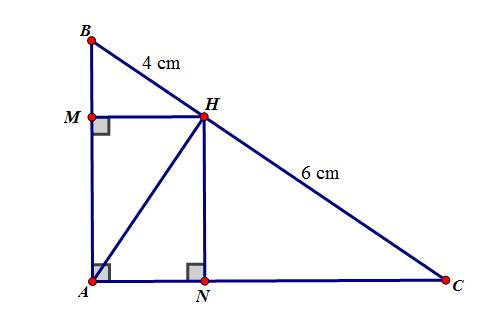
a, ΔABC vuông tại A \(\Rightarrow \angle BAC=90^o\)
M, N lần lượt là hình chiếu của H lên AB, AC \(\Rightarrow \angle HMA= \angle HNA =90^o \)
Tứ giác AMHN có: \(\angle BAC=\angle HMA=\angle HNA=90^o\)
Suy ra AMHN là hình chữ nhật.
b, Có: ΔAHB ∼ ΔCAB (g.g) \(\Rightarrow AB^2=BH.BC=4.(4+6)=40 \Rightarrow AB=2\sqrt{10}\)(cm)
Có: ΔAHC ∼ ΔBAC (g.g) \(\Rightarrow AC^2=CH.CB=6.(6+4)=60 \Rightarrow AC=2\sqrt{15}(cm)\)
SΔABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.2.\sqrt{10}.2.\sqrt{15}=10\sqrt{6}\)(cm2)

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
b: BC=10cm
AH=4,8cm
BH=3,6cm
CH=6,4cm

A B C 8 15 H M N 8
a, Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2+AC^2=BC^2\Rightarrow BC^2=64+225=289\Rightarrow BC=17\)cm
Xét tam giác AHC và tam giác BAC ta có :
^AHC = ^BAC = 900
^C _ chung
Vậy tam giác AHC ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{AH}{AB}=\frac{AC}{BC}\)( tỉ số đồng dạng )
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.15}{17}=\frac{120}{17}\)cm
b, Vì MH vuông AB
NA vuông AB
=> MH // NA tương tự ta có : MH // AN
=> tứ giác AMNH là hình bình hành
mà ^HNA = 900 ; ^BAC = 900 ; ^HMA = 900
=> tứ giác AMHN là hình vuông