Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABD có:
AD = AB (giả thiết)
=> Tam giác ABD là tam giác cân
=> Góc B = góc D (t/chất của tam giác cân)
Có: Q là tr/điểm AD
M là tr/điểm AB
=> QM // BD (t/chất đg tr/bình của tam giác)
=>Tứ giác QMBD là hình thang
Mà: Góc B = góc D (tam giác ABD là tam giác cân)
=> Hình thang QMBD là hình thang cân
P/s: Mình giải đến đây thôi. Mình thấy câu b "có j đó sai sai"?! Chẳng phải ở trên đã nói M là tr/điểm của AB rồi sao?! Sao ở câu b lại nói I là tr/điểm của AB?! Mình chưa giải câu c vì mik nghĩ đáp án câu b có thế sẽ là manh mối để giải câu c. Mình mong nếu bạn viết nhầm thì mau mau sửa lại để mik giải tiếp!!!! Thân.![]()

A B C D M N P Q
a
Do:
MQ là đường trung bình của tam giác ABD nên MQ//BD và MQ=BD/2 (1)
NP là đường trung bình của tam giác CBD nên NP//BD và NP=BD/2 (2)
Từ (1) và (2) suy ra điều phải chứng minh ( có 2 cặp cạnh đối song song và bằng nhau )
b
MNPQ là hình chữ nhật nên QM vuông góc với MN.
Khi đó AC vuông góc với BD.
Vậy hình thang ABCD cần thêm điều kiện AC vuông góc với BD thì MNPQ là hình chữ nhật.

Bài 2 :
A B C D M E
a, Xét tam giác ABC ta có :
D là trung điểm AB
M là trung điểm CB
=)) DM là đường TB tam giác ABC
=)) DM // AC hay DM // AE (1)
Ta có : E là trung điểm AC
M là trung điểm BA
=)) EM là đường TB tam giác ABC
=)) EM // AB hay EM // AD (2)
Từ 1;2 =)) Tứ giác ADME là hình bình hành
b, Nếu tam giác ABC cân tại A => AM là đường trung tuyến AM
=)) AM đồng thời là tia phân giác của ^A
Xét hình bình hành ADME có 2 đường chéo AM là tia phân giác của ^A (cmt)
=)) Tứ giác ADME là hình thoi
c, Nếu tam giác ABC vuông tại A => ^A = 90^0
Xét hình bình hành ADME có ^A =90^0
=)) Tứ giác ADME là hình chữ nhật

2/
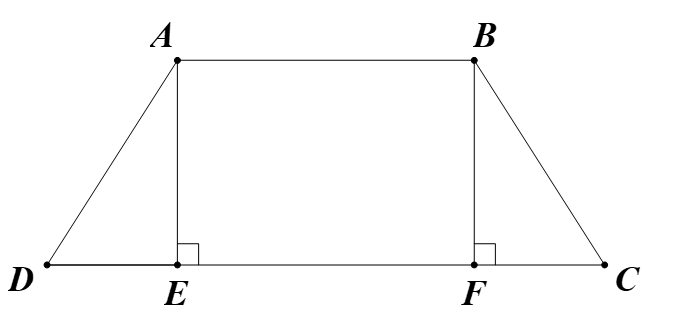
a/ hình thang ABCD có
AB // EF
==> AB // KF
xét tam giác ABC có
F là trung điểm của BC
AB // KF
==> KF là đường trung bình của tam giác ABC
==> K là trung điểm của AC
==> AK = KC
b/
E là trung điểm AD
F là trung điểm BC
==> EF là đường trung bình của hình thang ABCD
==> EF = (AB + CD) / 2 = (4 + 10) / 2 = 7(cm)
KF là đường trung bình của tam giác ABC nên
KF = AB / 2 = 4 / 2 = 2(cm)
==> EK = EF - KF = 7 - 2 = 5(cm)
vậy EK = 5(cm), KF = 2 (cm)
3/
a/ ta có
D là trung điểm của AB
M là trung điểm của BC
==> DM là đường trung bình của tam giác ABC
==> Dm // AC
==> DM // AE ( E thuộc AC, DM // AC)
chứng minh tương tự ta có
ME là đường trung bình của tam giác ABC
==> AD // ME
tứ giác ADME có DM // AE, AD // ME nên là HBH
b/ ( nếu tam giác ABC cân tại A)
tam giác ABC cân tại A ==> AB = AC
AD = 1/2 AB (D là trung điểm của AB)
AE = 1/2 AC (E là trung điểm của AC)
==> AD = AE
c/ (nếu tam giác ABC vuông)
ta có
tứ giác ADME là HBH
góc A = 90 độ
==> tứ giác ADME là HCN
d/ ta có
AB^2 + AC^2 = BC^2
6^2 + 8^2 = 100
==> BC = 10(cm)
AM là đường trung tuyến của tam giác ABC
==> AM = 1/2 BC = 1/2 . 10 = 5(cm)
vậy AM = 5cm
Bài 2:Cho mk ý kiến,sai đề à???4cm=6cm nhé

Bài 3:

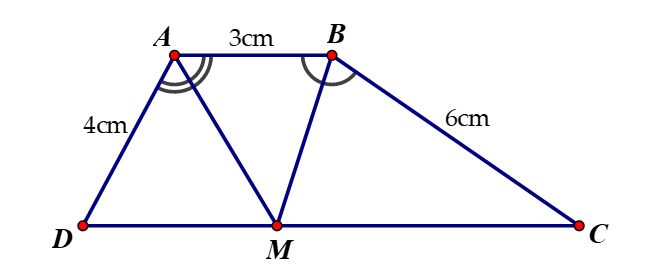
Bài 4:
Nối D với E, nối D với M:
Chứng minh được ED//FB (BEDF là hình thoi) (1)
BF là đường trung bình tam giác AMD
=> MD//FB (tc) (2)
(1),(2) => MD trùng với ED (định lý) ( Qua 1 điểm ko thuộc đường thẳng a có 1 và chỉ 1 đường thẳng đi qua điểm đó và song song với đường thẳng a )
từ đó bạn có thể cm BMCD là hình chữ nhật ( nếu cần )
( xét từ1 giác BDCM có BC cắt DM tại trung điểm của mỗi đoạn ->BMCD là Hình chữ nhật)
Bài 5:

6,5cm