Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có : tam giác ABC vuông tại A
=> góc B + góc C = 90\(^o\)
Mà góc B = 53\(^o\)
=> góc C = góc A - góc B
=> góc C = 90\(^o\)- 53\(^o\)
=> góc C = 37\(^o\)
b) Xét tam giác BEA và tam giác BED có :
BD = BA (gt)
BE là cạnh chung
góc ABE = góc DBE ( BE là tia p/giác của góc B)
=> tam giác BEA = tam giác BED
c) Ta có CH vuông góc với BE
=> Tam giác BHC và tam giác BHF là tam giác vuông
Xét tam giác vuông BHF và tam giác vuông BHC có:
BH là cạnh chung
góc FBH = góc HBC ( BE là tia p/giác của góc B)
=> tam giác vuông BHF = tam giác vuông BHC ( cạnh góc vuông + góc nhọn )
=> BF = BC ( 2 cạnh tương ứng ) (*)
d) Xét tam giác BEF và tam giác BEC có :
BF = BC ( theo (*))
góc FBE = góc CBE ( BE là tia p/giác của góc B)
BE là cạnh chung
=> tam giác BEF = tam giác BEC (c . g . c )
=> góc BFD = góc BCA ( 2 góc tương ứng ) (**)
Xét tam giác BAC và tam giác BDF có :
góc BFD = góc BCA ( theo (**))
góc B là góc chung
BA = BD (gt)
=> tam giác BAC = tam giác BDF ( g . c . g )
=> góc FDB = góc CAB ( 2 góc tương ứng )
Xét tam giác BED có : góc EBD + góc BED + góc BDE = 180\(^o\)
Mà :góc FDB = góc CAB = 90\(^o\)
góc EBD = \(\frac{1}{2}\)góc B = \(\frac{53}{2}\)= 26,5\(^o\)
=> góc BED = 180\(^o\)- (90\(^o\)+ 26,5\(^o\))
=> góc BED = 180\(^o\)- 116,5\(^o\)
=> góc BED = 63,5\(^o\)
Mặt khác : Tam giác BED = tam giác BEA
=> góc AEB = BED = 63,5\(^o\)
Xét tam giác FAE có :góc FAE + góc FEA + góc AFE = 180\(^o\)
Mà : góc FAE = 90\(^o\), góc AFE = góc ACB = 37\(^o\)
=> FEA = 180\(^o\)- (90\(^o\)+ 37\(^o\))
=> FEA = 180\(^o\)- 127\(^o\)
=> FEA = 53\(^o\)
Lại có : góc FAD = góc FEA + góc AEB + góc BED
=> FAD = 53\(^o\)+ 63,5\(^o\)+ 63,5 \(^o\)
=> FAD = 180\(^o\)
=> D, F, E thẳng hàng

a: Xét ΔBEA và ΔBED có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBEA=ΔBED

a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
b: Xét ΔBFC có
BH là đường cao
BH là đường phân giác
Do đó: ΔBFC cân tại B
c: Ta có: ΔBFC cân tại B
=>BF=BC
Xét ΔBDF và ΔBAC có
BD=BA
\(\widehat{DBF}\) chung
BF=BC
Do đó: ΔBDF=ΔBAC
=>\(\widehat{BDF}=\widehat{BAC}=90^0\)
Ta có: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}\)
mà \(\widehat{BAE}=90^0\)
nên \(\widehat{BDE}=90^0\)
mà \(\widehat{BDF}=90^0\)
và DE,DF có điểm chung là D
nên D,E,F thẳng hàng

a: \(\widehat{ABC}=50^0\)
b Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE

a,
Xét tam giác vuông ABC có:
góc BAC=90°(gt)
góc B=53°(gt)
=>góc ACB=90°-53°=37°
b,
Xét tam giác BAE và tam giác BDE có:
BA=BD(gt)
góc DBE=góc ABE(BE là phân giác góc B)
BE cạnh chung
=>tam giác BAE=tam giác BDE(c.g.c) (1)
Lại do góc EAB=góc CAB=90°(gt)
Từ (1)=>góc EAB=góc EDB=90°
c,
Do CH_|_BE tại H(gt)
=>góc BHC=góc BHF=90°
Xét tam giác BHC và tam giác BHF có:
góc HBC=góc HBF=53/2=26,5°(BE là phân giác)
BH cạnh chung
góc HFB=góc HCB=90°-26,5°=63,5°
=>tam giác BHC=tam giác BHF(g.c.g)
d,
Tam giác Vuông BDF có:
góc DBF+góc DFB=90°
=>góc DFB=90°-53°=37°
Mà góc ACB=37°(cmt)
=>góc DFB=góc ACB=37°
Ta lại có:
BD=BA(gt)
góc CBH=góc HBF=26,5°
=>tam giác BAC=tam giác DBF(g.c.g)
Theo tổng 3 góc trong 1 tam giác,ta có:
-Trong tam giác vuông CDF có:
góc D=90°
góc C=63,5°
=>góc F=180°-(90+63,5)=26,5°
-trong tam giác vuông FHE có:
góc H=90°
góc F=26,5°(cmt)
=>góc HEF=180°-(90°+26,5)=63,5° (2)
-trong tam giác vuông CHE có:
góc H=90°
góc HCE=góc HCB-góc ACB
=63,5°-37°=26,5°
=>góc HEC=180°-(90°+26,5°)=63,5° (3)
-trong tam giác vuông EDC có:
góc D=90°
góc C=37°(cmt)
=>góc CED=180-(90°+37°)=53° (4)
Cộng (2),(3),(4) vế theo vế, ta được:
góc (HEF+HEC+CED)=63,5°+63,5°+53°=180°
=>3 điểm D,E,F thẳng hàng(đpcm)

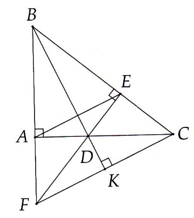

Câu hỏi của Phạm Thùy Dung - Toán lớp 7 - Học toán với OnlineMath
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).