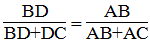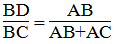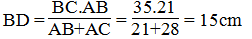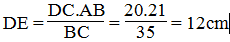Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Vì AD là phân giác nên \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow AB=\dfrac{BD.AC}{DC}=12cm\)
b, Vì DE // AB ta được \(\dfrac{CE}{AE}=\dfrac{CD}{BD}\)
Lại có AC/AB = DC/BD ( tỉ lệ thức của AD là pg)
\(\dfrac{CE}{AE}=\dfrac{AC}{AB}\Rightarrow CE.AB=AC.AE\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=212+282=1225BC2=AB2+AC2=212+282=1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠∠(BAC) nên:
(t/chất đường phân giác)
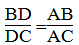
Suy ra: 
Hay 
Suy ra: 
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: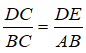 
(Hệ quả định lí Ta-lét)
Suy ra: 
a: BC=35(cm)
Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/21=CD/28
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó: BD=15(cm); CD=20(cm)
Xét ΔABC có ED//AB
nên ED/AB=CD/CB
=>ED/21=20/35=4/7
=>ED=12(cm)
a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
Hình bình hành AEDF có AD là phân giác của góc FAE
nên AEDF là hình thoi
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{CD}{DB}=\dfrac{AC}{AB}\left(1\right)\)
Xét ΔABC có DE//AB
nên \(\dfrac{CD}{DB}=\dfrac{CE}{EA}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AC}{AB}=\dfrac{EC}{EA}\)
=>\(AC\cdot AE=AB\cdot EC\)
a. -Xét △ABC: AD là đường phân giác (gt)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (định lí về đường phân giác trong tam giác)
\(\Rightarrow\dfrac{AB}{16}=\dfrac{6}{8}\)
\(\Rightarrow AB=\dfrac{6}{8}.16=12\left(cm\right)\)
b) -Xét △ABC: DE//AB (gt)
\(\Rightarrow\dfrac{EA}{EC}=\dfrac{BD}{CD}\) (định lí Ta-let)
Mà \(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(cmt\right)\)
\(\Rightarrow\dfrac{EA}{EC}=\dfrac{AB}{AC}\) nên \(AC.EA=AB.EC\)
c) -Ta có: \(\widehat{BAD}=\widehat{CAD}\) (AD là tia phân giác của \(\widehat{BAC}\))
Mà \(\widehat{BAD}=\widehat{ADE}\) (AB//DE và so le trong)
\(\Rightarrow\widehat{CAD}=\widehat{ADE}\) nên △ADE cân tại E.
\(\Rightarrow AE=DE\)
-Xét △AIE: AP là đường phân giác.
\(\Rightarrow\dfrac{PE}{PI}=\dfrac{AE}{AI}\)(định lí về đường phân giác trong tam giác)
Mà \(AE=DE\left(cmt\right)\); \(AI=BI\) (I là trung điểm AB)
\(\Rightarrow\dfrac{PE}{PI}=\dfrac{DE}{BI}\)
-Xét △QDE: DE//BI.
\(\Rightarrow\dfrac{QD}{QI}=\dfrac{DE}{BI}\) (hệ quả định lí Ta-let)
Mà \(\dfrac{PE}{PI}=\dfrac{DE}{BI}\) nên \(\dfrac{PE}{PI}=\dfrac{QD}{QI}\)