Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có : \(\dfrac{AB}{AC}=\dfrac{3}{4}=>\dfrac{3}{4}AC=AB\)
AB + AC = 21
3/4 AC + AC = 21
7/4 AC = 21
AC = 12 ( cm )
AB = 21 - 12 = 9 ( cm )
Áp dụng định lí Pytago vào tam giác , ta có :
BC ^ 2 = AB ^ 2 + AC ^ 2 = 12^2 + 9^2 = 225
-> BC = 15 ( cm )
b, Áp dụng hệ thức lượng :
AH . BC = AB . AC
-> AH = AB.AC / BC = \(\dfrac{9.12}{15}=7,2\left(cm\right)\)
AB^2 = BH . BC
-> BH = AB^2 / BC = \(\dfrac{81}{15}=5,4\left(cm\right)\)
AC^2 = HC . BC
-> HC = AC^2 / BC = \(\dfrac{144}{15}=9,6\left(cm\right)\)

Tam giác ABC vuông tại A, theo hệ thức lượng:
\(AB^2=BH.BC\)\(\Rightarrow BH=\frac{AB^2}{BC}\)(1)
\(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\frac{BH}{HC}=\frac{AB^2}{AC^2}=\frac{3^2}{4^2}=\frac{9}{16}\)
Đặt \(\frac{BH}{HC}=\frac{9}{16}=x\Rightarrow\hept{\begin{cases}BH=9x\\HX=16x\end{cases}}\)
\(BH+HC=BC\Leftrightarrow9x+16x=125\)
\(\Leftrightarrow x=5\)
\(\Rightarrow BH=45\left(cm\right);HC=80\left(cm\right)\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(AB=\dfrac{3}{7}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{3}{7}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{1}{42^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{49}AC^2}+\dfrac{\dfrac{9}{49}}{\dfrac{9}{49}AC^2}=\dfrac{1}{1764}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{49}=2088\)
\(\Leftrightarrow AC^2=11368\)
\(\Leftrightarrow AC=14\sqrt{58}\left(cm\right)\)
\(\Leftrightarrow AB=\dfrac{3}{7}\cdot14\sqrt{58}=6\sqrt{58}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2=13456\)
hay BC=116(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(6\sqrt{58}\right)^2}{116}=18\left(cm\right)\\CH=\dfrac{AC^2}{CH}=\dfrac{\left(14\sqrt{58}\right)^2}{116}=98\left(cm\right)\end{matrix}\right.\)

Giải tam giác nhé em, ta vần vận dụng định lý Pitago và các hệ thức lượng.
Áp dụng đl Pitago ta có: \(BC=\sqrt{AB^2+AC^2}=5\)
Áp dụng hệ thức lượng \(BH=\frac{AB^2}{BC}=1,8\Rightarrow CH=BC-BH=3,2\)
\(AH=\sqrt{BH.CH}=2,4\)
\(sinB=\frac{AC}{BC}=0,8\Rightarrow B\approx53^08'\Rightarrow C\approx36^052'\)

Có:
\(\dfrac{AB}{AC}=\dfrac{4}{3}=\dfrac{4k}{3k}\) (k là số bất kì)
\(\Rightarrow AB=4k,AC=3k\)
Áp dụng đl pytago vào tam giác ABC được:
\(BC^2=AB^2+AC^2=\left(4k\right)^2+\left(3k\right)^2=16k^2+9k^2=25k^2=\left(5k\right)^2\\ \Rightarrow BC=5k\left(cm\right)\)
Theo hệ thức lượng, có:
\(AH.BC=AB.AC\\ \Leftrightarrow3,6.5k=4k.3k\\ \Leftrightarrow18=12k\\ \Rightarrow k=\dfrac{18}{12}=\dfrac{3}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=4k=4.\dfrac{3}{2}=6\left(cm\right)\\AC=3k=3.\dfrac{3}{2}=\dfrac{9}{2}=4,5\left(cm\right)\\BC=5k=5.\dfrac{3}{2}=\dfrac{15}{2}=7,5\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow P_{ABC}=AB+AC+BC=6+4,5+7,5=18\left(cm\right)\)

Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
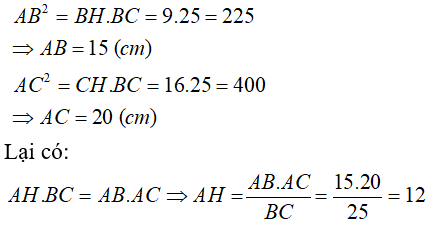
Bài này mk chỉ làm đk theo 2 cách thôi nha , tại cách thứ 3 mk quên ko ghi vô vở rồi :
Cách 1 :
Gọi độ dài các cgv là : AB = 3x
AC = 4x
ADĐL pitago vào tam giác vuông ABC , có :
BC2 = AB2 + AC2
1252 = (3x)2 + (4x)2
1252 = 9x2 + 16x2
15625 = 25x2
x2 = 625
=> x = 25
=> AB= 3x = 3 . 25 = 75 cm
AC = 4x = 4 . 25 = 100 cm
ADHT về cgv và đ/c trong tam giác vuông ABC , ta có :
AB2 = BH . BC
752 = BH . 125
BH = 45 cm
Ta có : BC = BH + HC
125 = 25 + HC
HC = 80 cm
Cách 2 :
Ta có : \(\dfrac{AB}{AC}\)= \(\dfrac{3}{4}\)
<=> \(\dfrac{AB}{3}\) = \(\dfrac{AC}{4}\) <=> \(\left(\dfrac{AB}{3}\right)^2\)= \(\left(\dfrac{AC}{4}\right)^2\)
<=> \(\dfrac{AB^2}{9}\)= \(\dfrac{AC^2}{16}\)
<=> \(\dfrac{AB^2+AC^2}{25}\)= \(\dfrac{BC^2}{25}\)
<=> \(\dfrac{125^2}{25}\) = \(\dfrac{15625}{25}\)= 625
Ta có : \(\dfrac{AB^2}{9}\)= \(\dfrac{AC^2}{16}\)= 625
<=> \(\dfrac{AB^2}{9}\)= 625
=> AB2 = 5625
=> AB = 75 cm
<=> \(\dfrac{AC^2}{16}\)= 625
=> AC2 = 10000
=> AC = 100 cm
BH và HC tính tương tự cách 1