Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

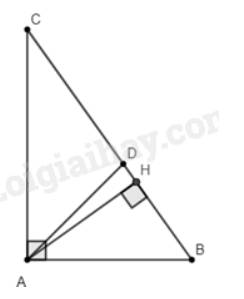
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).

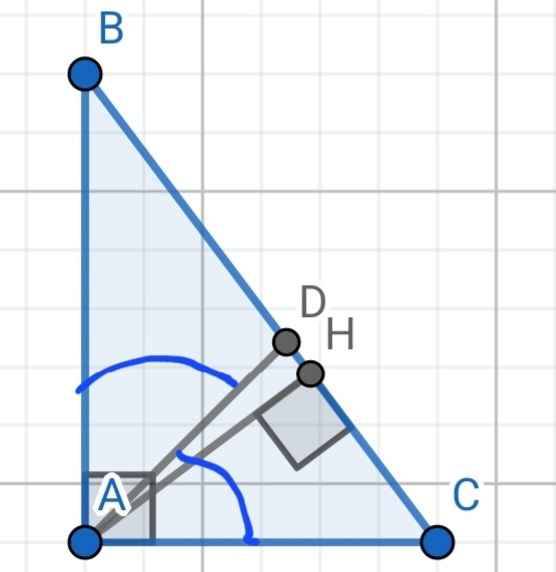
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA

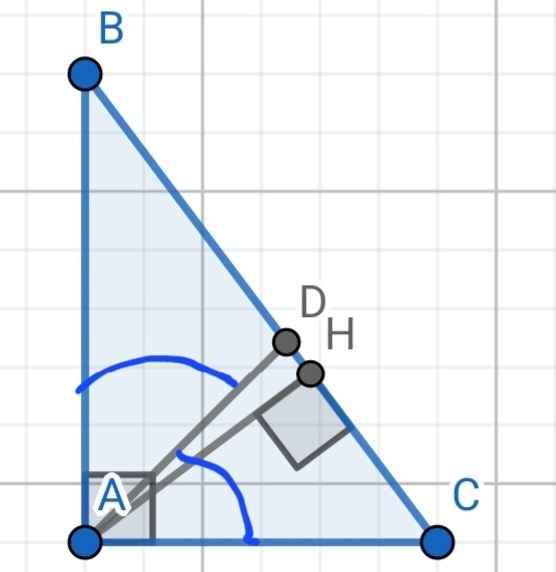
a) Do AD là phân giác của ∠A
⇒ DB/DC = 8/6 = 4/3
b) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠HAB = ∠HCA (cùng phụ ∠B)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/CH = AB/CA
a: DB/DC=AB/AC=4/3
b: Sửa đề: AH/CA=AB/BC
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)
=>AH*BC=AB*AC
=>AH/AC=AB/CB

a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

a: BC=căn 6^2+8^2=10cm
b: AD là phân giác
=>DB/Ab=DC/AC
=>DB/3=DC/4
mà DB+DC=10
nên DB/3=DC/4=10/(3+4)=10/7
=>DB=30/7cm

a: \(CB=\sqrt{6^2+8^2}=10\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=10/7
=>BD=30/7cm; CD=40/7cm
b: \(AH=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\)