Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=92+122=225
BC=15cm
* AH.BC=AB.AC
AH.15=9.12
AH.15=108
AH=7,2cm
\(sinB=\dfrac{4}{5};cosB=\dfrac{3}{5};tanB=\dfrac{4}{3};cotanb=\dfrac{3}{4}\)
\(=>sinC=\dfrac{3}{5};cosC=\dfrac{4}{5};tanC=\dfrac{3}{4};cotanC=\dfrac{4}{3}\)
b)
tam giác ABC vuông tại A có
AC.AK=AH2
HB.HC=AH2
=>AC.AK=HB.HC
\(=>\dfrac{AC}{HC}=\dfrac{HB}{AK}\)

cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C

A B C H
a) Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=5^2+12^2=169\)
\(\Leftrightarrow\)\(BC=13\)
b) Áp dụng hệ thức lượng ta có:
\(AB.AC=BC.AH\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}=4\frac{8}{13}\)
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BH=\frac{AB^2}{BC}=\frac{25}{13}\)
c) \(sinB=\frac{AC}{BC}=\frac{12}{13}\) \(tanB=\frac{AC}{AB}=\frac{12}{5}\)
\(cosB=\frac{AB}{BC}=\frac{5}{13}\) \(cotB=\frac{AB}{AC}=\frac{5}{12}\)

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=21\\AC^2=28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{21}\left(cm\right)\\AC=2\sqrt{7}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2\sqrt{7}}{7}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{\sqrt{21}}{7}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2\sqrt{7}}{\sqrt{21}}=\dfrac{2\sqrt{3}}{3}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{\sqrt{21}}{2\sqrt{7}}=\dfrac{\sqrt{3}}{2}\)

A B C H
a) Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=5^2+12^2=169\)
\(\Leftrightarrow\)\(BC=13\)
b) ÁP dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Rightarrow\)\(AH=\frac{AB.AC}{BC}=\frac{5.12}{13}=\frac{60}{13}\)
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BH=\frac{AB^2}{BC}=\frac{25}{13}\)
c) \(sinB=\frac{AC}{BC}=\frac{12}{13}\) \(cos=\frac{AB}{BC}=\frac{5}{13}\)
\(tanB=\frac{AC}{AB}=\frac{12}{5}\) \(cotB=\frac{AB}{AC}=\frac{5}{12}\)

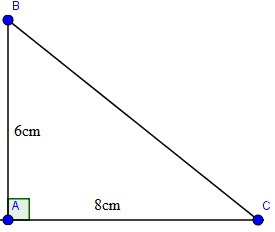
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2=AB2+AC2=62+82=100BC2=AB2+AC2=62+82=100
Suy ra: BC = 10 (cm)
Ta có:
sinˆB=ACBC=810=0,8sinB^=ACBC=810=0,8
cosˆB=ABBC=610=0,6cosB^=ABBC=610=0,6
tgˆB=ACAB=86=43tgB^=ACAB=86=43
cotgˆC=tgˆB=43

\(BC^2=AB^2+AC^2=36+64=100=10^2\)
\(\Rightarrow BC=10\left(cm\right)\)
\(SinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow SinC=Sin\left(90-B\right)=CosB=\dfrac{3}{5}\)
\(CosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow CosC=Cos\left(90-B\right)=SinB=\dfrac{4}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow tanC=tan\left(90-B\right)=CotB=\dfrac{3}{4}\)
\(CotB=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow cotC=cot\left(90-B\right)=tanB=\dfrac{4}{3}\)
Giải: