Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\dfrac{{AG}}{{AM}} = \dfrac{6}{9} = \dfrac{2}{3}\);
\(\dfrac{{BG}}{{BN}} = \dfrac{4}{6} = \dfrac{2}{3}\);
\(\dfrac{{CG}}{{CP}} = \dfrac{4}{6} = \dfrac{2}{3}\).

Bài làm
Ta có: \(AG=\frac{2}{3}AM\)
\(CG=\frac{2}{3}CP\)
\(BG=\frac{2}{3}BN\)
Mà AG = BG = CG
=> \(\frac{2}{3}AM=\frac{2}{3}CP=\frac{2}{3}BN\)
=> \(AM=CP=BN\)
Vì AG = GC ( gt )
=> Tam giác AGC cân tại G
Mà BN là đường trung tuyến và G thuộc BN
=> GN cũng là đường trung tuyến
=> GN là đường cao ( do tam giác AGC cân ở G )
=> Tam giác ABC cân ở B
=> AB = BC (1)
Vì AG = GB ( gt )
=> Tam goác AGB cân tại G
Mà CP là đường trung tuyến và G thuộc CP
=> GN là đường trung tuyến
Và GN cũng là đường trung tuyến của tam giác cân AGC
=> GN cũng là đường cao
=> CP cũng là đường cao.
=> Tam giác ACB cân ở C
=> AC = BC (2)
Vì BG = GC ( gt )
=> Tam giác BGC cân tại G
Mà AM là đường trung tuyến và G thuộc AM
=> GM cũng là đường trung tuyến của tam giác GBC
Và GM là đường cao
=> AM cũng là đường cao
=> Tam giác ABC cân ở A
=> AB = AC (3)
Từ (1) và (2) và (3) => AB = AC = BC
=> Tam giác ABC đều.
# Học tốt #
A B C N P M G
Ta có: AG = GB (gt) => t/giác AGB cân tại G có GN là đường trung tuyến
=> GN cũng là đường cao của t/giác AGB
Hay CN là đường cao của t/giác ABC (Do C, G, N | | | )
mà CN cũng là đường trung tuyến
=> t/giác ACB cân tại C => AC = CB (1)
BG = GC (gt) => t/giác BGC cân tại G có GM là đường trung tuyến
=> GM cũng là đường cao của t/giác GBC
hay AM là đường cao của t/giác ABC (Do A; G; M | | | )
mà AM cũng là đường trung tuyến của t/giác ABC
=> t/giác ABC cân tại A => AB = AC (2)
Từ (1) và (2) => AB = AC = BC
=> t/giác ABC đều

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
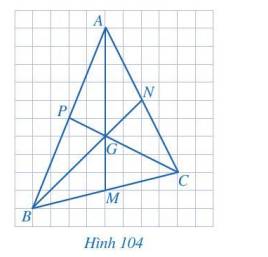

Vì G là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\)
Ta có: \(GN = BN – BG = BN - \dfrac{2}{3}BN = \dfrac{1}{3}BN;\\ GP = CP – CG = CP - \dfrac{2}{3}CP = \dfrac{1}{3}CP\)
Do đó, \(BN = 3. GN ; CP = 3. GP\)
Như vậy, \(BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN;\\CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP\)
Vậy \(BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP\);
\(BG = 2GN; CG = 2GP\).