Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

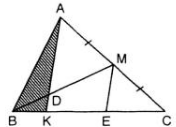
a) Xét tg ADM và tg ECB: ADM^ = EDB^ (đđ) ; MAD^ = BED^ (slt)
=> tg ADM đd tg ECB (g.g)
=> \(\dfrac{AM}{BE}=\dfrac{DM}{BD}=2\) \(\Rightarrow BE=\dfrac{AM}{2}\)
Thay \(BE=\dfrac{AM}{2}\) và AC = 2AM vào tỉ số BE/AC, được:
\(\dfrac{BE}{AC}=\dfrac{\dfrac{AM}{2}}{2AM}=\dfrac{1}{4}\)
b) xét tg AKC và tg EKB: AKC^ = EKB^ (đđ) ; CAK^ = BEK^ (slt)
=> tg AKC đd tg EKB (g.g)
=> \(\dfrac{BE}{AC}=\dfrac{BK}{KC}=\dfrac{1}{4}\) \(\Rightarrow KC=4BK\)
Mà BC = BK + KC => BC = 5BK hay BK/BC = 1/5
c) (nếu giải được thì t gửi cho- hình tự vẽ nhe ^^!)

a/ Xét tg ADM và tg EDB
Bx//AC \(\Rightarrow\widehat{DAC}=\widehat{DEB}\) (góc so le trong)
\(\widehat{ADM}=\widehat{BDE}\) (góc đối đỉnh)
=> Xét tg ADM đồng dạng tg EDB (g.g.g) \(\Rightarrow\frac{BD}{DM}=\frac{BE}{AM}=\frac{BE}{\frac{AC}{2}}=\frac{1}{2}\Rightarrow\frac{BE}{AC}=\frac{1}{4}\)
b/ Xét tg BKE và tg AKC có
\(\widehat{AKC}=\widehat{BKE}\) (góc đối dỉnh)
Bx//AC \(\Rightarrow\widehat{KAC}=\widehat{KEB}\) (góc so le trong)
=> tg BKE đồng dạng tg AKC (g.g.g) \(\Rightarrow\frac{BE}{AC}=\frac{BK}{KC}=\frac{1}{4}\Rightarrow\frac{BK}{AC}=\frac{1}{5}\left(dpcm\right)\)

a: Xét ΔDBE và ΔDMA có
góc DBE=góc DMA
góc BDE=góc MDA
=>ΔDBE đồng dạng vơi ΔDMA
=>BE/MA=DB/DM=1/3
=>BE=1/3MA=1/3*1/2AC=1/6AC
b: BE//AC
=>BK/KC=BE/AC=1/4
=>BK/BC=1/5