Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

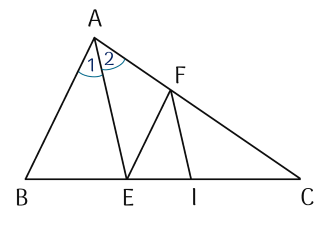
1) \widehat{{BAE}}=\widehat{{EAC}}BAE=EAC (giả thiết). (1)
Vì {AB}AB // {EF}EF nên \widehat{{BAE}}=\widehat{{AEF}}BAE=AEF (hai góc so le trong). (2)
Vì AEAE // FIFI nên \widehat{EAC}=\widehat{IFC}EAC=IFC (hai góc đồng vị). (3)
Vì {AE}AE // {FI}FI nên \widehat{{AEF}}=\widehat{{EFI}}AEF=EFI (hai góc so le trong). (4)
Từ (1), (2), (3), (4) suy ra: \widehat{{BAE}}=\widehat{{EAC}}=\widehat{{AEF}}=\widehat{{IFC}}=\widehat{{EFI}}BAE=EAC=AEF=IFC=EFI.
2) Từ chứng minh trên, ta có: \widehat{{EFI}}=\widehat{{IFC}}EFI=IFC mà {FI}FI là tia nằm giữa hai tia {FE}FE và {FC}FC.
Vậy {FI}FI là tia phân giác của \widehat{{EFC}}EFC.

*Tự vẽ hình
a) Có : DE//BC(GT)
EF//AB(GT)
=> BDEF là hình bình hành
=> BD=EF
Mà : AD=DB(GT)
=> AD=EF (đccm)
b) Ta có : AD=DB(GT)
DE//BC (GT)
=> DE là đường trung bình của tam giác ABC
=> AE=EC
Có : AE=EC(cmt)
EF//AB(GT)
=> EF là đường trung bình của tam giác ABC
=> BF=FC
Mà : BF=DE(BDEF-hình bình hành)
=> FC=DE
Xét tam giác ADE và EFC có :
AE=EC(cmt)
AD=EF(cm ý a)
DE=FC(cmt)
=> Tam giác ADE=EFC(c.c.c)
c) Đã chứng minh ở ý b
*Cách khác:
Giải:
Hình bạn tự vẽ nhé.
a) Ta có: BD // EF (vì AB /// EF)
=> Góc BDF = góc DFE (2 góc so le trong)
Vì DE // BC (gt)
nên góc EDF = góc BFD (2 góc so le trong)
Xét tam giác EDF và tam giác BDF có:
Góc BDF = góc DFE (chứng minh trên)
DF là cạnh chung
Góc EDF = góc BFD (chứng minh trên)
=> Tam giác DEF = tam giác FBD (g.c.g)
=> BD = EF ( 2 cạnh tương ứng) (đpcm)
Mà BD = AD (vì D là trung điểm của AB)
=> AD = EF (đpcm)
b) Ta có: AB // EF (gt)
=> Góc A = góc CEF (2 góc đồng vị)
Lại có: tam giác DEF = tam giác FBD (chứng minh trên)
=> Góc DEF = góc B (2 góc tương ứng) (1)
Mà DE // BC (gt)
=> Góc DEF = góc CFE (2 góc so le trong) (2)
Góc ADE = góc B (2 góc đồng vị)
Từ (1), (2) => Góc B = góc CFE
Mà góc B = góc ADE (chứng minh trên)
=> Góc ADE = góc CFE
Xét tam giác ADE và tam giác CEF có:
Góc CEF = góc A (chứng minh trên)
AD = EF (chứng minh trên)
Góc ADE = góc CFE (chứng minh trên)
=> Tam giác ADE = tam giác EFC (g.c.g) (đpcm)
c) Ta có: tam giác ADE = tam giác EFC (chứng minh trên)
=> AE = CE (2 cạnh tương ứng) (đpcm)

????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
a) Là chứng minh góc phải ko bạn???
đúng r bạn