Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)\(\Delta\)ABC có E là trung điểm của AB, D là trung điểm của AC nên ED là đường trung bình của tam giác => ED//BC
Tứ giác EDCB có ED//BC nên là hình thang (đpcm)
2) Hình thang EDCB có M, N lần lượt là trung điểm của BE và CD nên MN là đường trung bình của hình thang => MN // ED hay \(\hept{\begin{cases}NK//ED\\MI//ED\end{cases}}\)
\(\Delta\)BED có M là trung điểm của BE và MI//ED nên I là trung điểm của BD
Tương tự ta suy ra được K là trung điểm của CE
c) Ta có: IK = IN - KN = 1/2BC - 1/2ED = \(\frac{BC-ED}{2}=\frac{BC-\frac{BC}{2}}{2}=\frac{\frac{BC}{2}}{2}=\frac{BC}{4}\)
\(KN=MI=\frac{ED}{2}=\frac{\frac{BC}{2}}{2}=\frac{BC}{4}\)
Từ đó suy ra MI = IK = KN (đpcm)

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Dương Ánh Ngọc - Toán lớp 8 - Học toán với OnlineMath

\(a,\left\{{}\begin{matrix}AE=EB\\AD=DC\end{matrix}\right.\Rightarrow ED\) là đtb tam giác ABC
\(\Rightarrow ED=\dfrac{1}{2}BC;ED//BC\Rightarrow BEDC\) là hthang
\(b,\left\{{}\begin{matrix}EM=MB\\DN=NC\end{matrix}\right.\Rightarrow MN\) là đtb hthang BEDC
\(\Rightarrow MN//DE//BC;MN=\dfrac{DE+BC}{2}\)
Mà \(EM=MB\Rightarrow BI=ID\Rightarrow MI\) là đtb tam giác BED
\(\Rightarrow MI=\dfrac{1}{2}DE=0,5DE=\dfrac{1}{2}\cdot\dfrac{1}{2}BC=\dfrac{1}{4}BC=0,25BC\)
\(c,\) \(\left\{{}\begin{matrix}NK//ED\\DN=NC\end{matrix}\right.\Rightarrow EK=KC\Rightarrow KN\) là đtb tam giác EDC
\(\Rightarrow KN=\dfrac{1}{2}ED=MI\left(1\right)\)
\(IK=MN-MI-KN=\dfrac{ED+BC}{2}-\dfrac{ED}{2}-\dfrac{ED}{2}\\ =\dfrac{BC-DE}{2}=\dfrac{2DE-DE}{2}=\dfrac{DE}{2}=MI=KN\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow MI=IK=KN\)
\(d,IN=NK+KI=\dfrac{1}{2}DE+\dfrac{1}{2}DE=DE;IN//DE\left(MN//DE\right)\)
\(\Rightarrow EDNI\) là hbh nên \(EI=ND\)

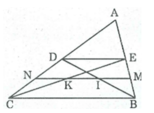
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
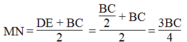
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC