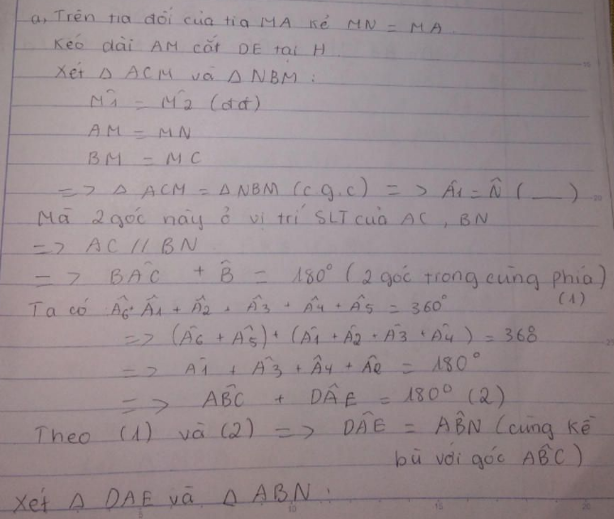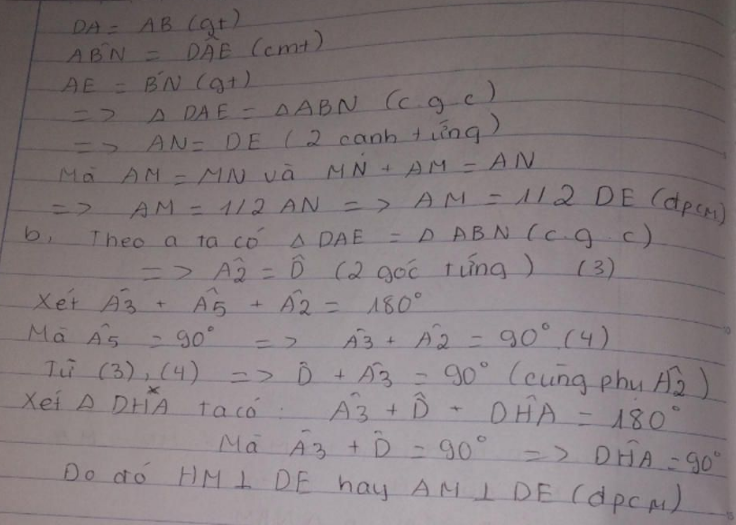Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình không vẽ hình, bạn tự vẽ nhé!
a) M là trung điểm của BC \(\Rightarrow BM=MC\)
Xét \(\Delta BAM\)và \(\Delta CDM\)có:
MA=MD ( giả thiết )
\(\widehat{BMA}=\widehat{CMD}\)( tính chất đối đỉnh )
BM=MC ( chứng minh trên )
\(\Rightarrow\Delta BAM=\Delta CDM\)( c.g.c )
b) Xét \(\Delta ACM\)và \(\Delta DBM\)có:
MA=MD ( giả thiết )
\(\widehat{BMD}=\widehat{CMA}\)( tính chất đối đỉnh )
BM=MC ( chứng minh trên )
\(\Rightarrow\Delta ACM=\Delta DBM\)( c.g.c )
\(\Rightarrow AC=BD\)( 2 cạnh tương ứng )
\(\Rightarrow\widehat{MAC}=\widehat{MDB}\)( 2 góc tương ứng ) ở vị trí so lê trong
\(\Rightarrow\)AC//BD
c) Đề bài không rõ ràng mình không làm được
d) Đề bài không rõ ràng mình không làm được
Chúc bạn học tốt!

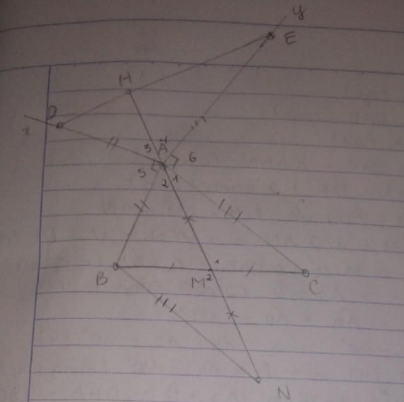
a) Kẻ MN là tia đối của tia MA và MN = MA
Kéo dài AM cắt DE tại H
Xét ΔΔAMC và ΔΔNMB có:
AM = NM (cho ở trên)
AMCˆAMC^ = NMBˆNMB^ (đối đỉnh)
MC = MB (suy từ gt)
=> ΔΔAMC = ΔΔNMB (c.g.c)
=> ACMˆACM^ = NBMˆNBM^ (2 góc t/ư)
mà 2 góc này ở vị trí so le trong nên AC // BN
=> BACˆBAC^ + ABNˆABN^ = 180o (trong cùng phía) (3)
Vì DA ⊥⊥ AB nên DABˆDAB^ = 90o;
EA ⊥⊥ AC nên EACˆEAC^ = 90o
Ta có: DAHˆDAH^ + DABˆDAB^ + BANˆBAN^ = 180o
=> DAHˆDAH^ + 90o + BANˆBAN^ = 180o
=> DAHˆDAH^ + BANˆBAN^ = 90o (1)
Lại có: EAHˆEAH^ + EACˆEAC^ + CANˆCAN^ = 180o
=> EAHˆEAH^ + 90o + CANˆCAN^ = 180o
=> EAHˆEAH^ + CANˆCAN^ = 90o (2)
Cộng vế (1) và (2) ta đc:
DAHˆDAH^ + BANˆBAN^ + EAHˆEAH^ + CANˆCAN^ = 90o + 90o
=> (DAHˆDAH^ + EAHˆEAH^) +(BANˆBAN^ + CANˆCAN^) = 180o
=> DAEˆDAE^ + BACˆBAC^ = 180o (4)
Từ (3) và (4) suy ra:
BACˆBAC^ + ABNˆABN^ = DAEˆDAE^ + BACˆBAC^
=> ABNˆABN^ = DAEˆDAE^
Do ΔΔAMC = ΔΔNMB (c/m trên)
=> AC = NB (2 cạnh t/ư)
mà AC = AE (gt)
=> NB = AE
Xét ΔΔABN và ΔΔDAE có:
AB = DA (gt)
ABNˆABN^ = DAEˆDAE^ (c/m trên)
NB = AE (c/m trên)
=> ΔΔABN = ΔΔDAE (c.g.c)
=> AN = DE 92 cạnh t/ư)
mà AM = 1212 AN nên AM = 1212 DE.