Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: ΔABC cân tại A
a:ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
=>AD vuông góc BC
b: Xét ΔAFI và ΔAEI có
AF=AE
góc FAI=góc EAI
AI chung
=>ΔAFI=ΔAEI
=>góc AFI=góc AEI
=>FI vuông góc AB
c: Xét ΔABC có
BE,AD là đường cao
BE cắt AD tại I
=>I là trực tâm
=>CI vuông góc AB
=>C,I,F thẳng hàng

A B C D E F G
Đề thiếu E là trung điểm của AB, F là trung điểm của AD
Gọi G là trung điểm của đoạn thẳng AC
Vì E là trung điểm của AB và F là trung điểm của AD
=> EF là đường trung bình của tg ABD
=> EF // BD (1)
C/m tương tự ta có EG // BC (2) và FG // DC (3)
mặt khác ta có AC vuông góc với BD và từ (1) => AC vuông góc với EF => AC là 1 đường cao của tam giác EFG (4)
C/m tương tự ta có FK vuông góc với EG và EH vuông góc FG lần lượt suy ra FK, EH cũng là đường cao của tam giác EFG (5)
Từ (4) và (5) => AC, FK, EH đồng quy ( đpcm )

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
BA=BE
=>B nằm trên trung trực của AE(1)
DA=DE
=>D nằm trên trung trực của AE(2)
Từ (1), (2) suy ra BD là đường trung trực của AE
=>BD vuông góc AE

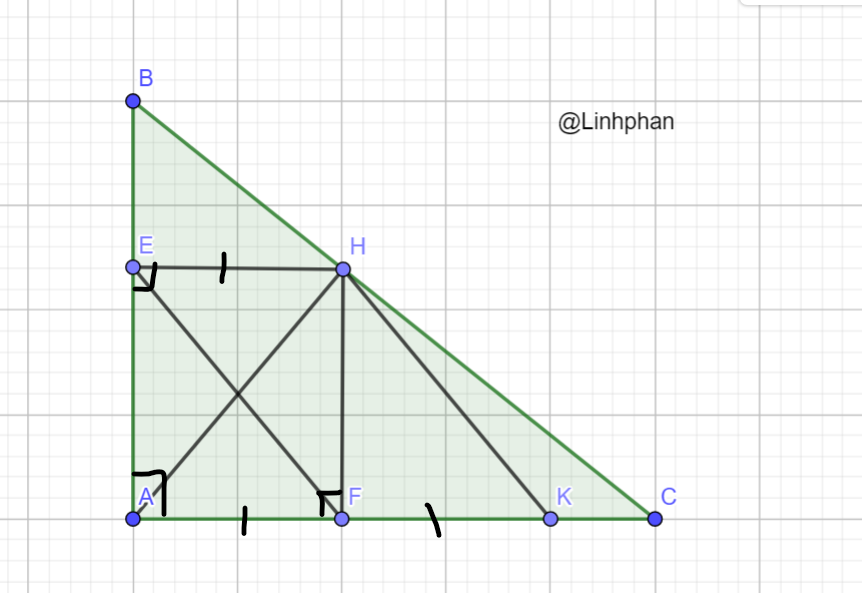
a, Vì HE ⊥ AB ; FA ⊥ AB => HE // FA (từ ⊥ đến // )
+, EA ⊥ AC ; HF ⊥ AC => EA // HF (từ ⊥ đến // )
Xét tứ giác AEHF có: HE // FA (cmt) ; EA // HF (cmt)
=> Tứ giác AEHF là hình bình hành (dhnb)
mà \(\hat{EAF} =90^0\)
=> Tứ giác AEHF là hình chữ nhật
=> AH = EF
b, Vì AEHF là hình chữ nhật (cmt)
=> EH//AF; EH = AF mà AF= FK (gt)
=> EH = FK
+, Xét tứ giác EHKF có: EH = FK (cmt)
EH // FK (do EH // AF; K ∈ AF)
=> Tứ giác EHKF là hình bình hành (dhnb)

