Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc EAB chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF và AE/AB=AF/AC
b: XétΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng với ΔABC

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AB*AF=AC*AE và AB/AE=AC/AF
b: Xét ΔABC và ΔAEF có
AB/AE=AC/AF
góc BAC chung
=>ΔABC đồng dạng với ΔAEF

a) Xét \(\Delta CAF\) và \(\Delta BAE\) có:
\(\widehat{CFA}=\widehat{BEA}=90^0\)
\(\widehat{BAC}:\) chung
suy ra: \(\Delta CAF~\Delta BAE\)
\(\Rightarrow\)\(\frac{AF}{AE}=\frac{AC}{AB}\)\(\Rightarrow\) \(AE.AC=AF.AB\) (ĐPCM)
\(\Rightarrow\)\(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét \(\Delta AEF\)và \(\Delta ABC\) có:
\(\frac{AE}{AB}=\frac{AF}{AC}\)
\(\widehat{BAC}\) CHUNG
suy ra: \(\Delta AEF~\Delta ABC\)



Bài giảng học thử
Video không hỗ trỡ trên thiết bị của bạn!
Bài 9: Hình chữ nhật - Phần 1 - Toán 8 - Cô Diệu Linh
Video không hỗ trỡ trên thiết bị của bạn!
Bài 1. Định lí Ta-lét trong tam giác - Phần 1 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Đường trung bình của tam giác, của hình thang - Phần 2 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 3. Hình thang cân - Phần 3 - Toán 8 - Thầy Phan Toàn
Video không hỗ trỡ trên thiết bị của bạn!
Bài 4. Khái niệm hai tam giác đồng dạng - Phần 2 - Toán 8 - Thầy Phan Toàn

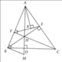
A B C E F H I
Giải
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (vì đối đỉnh)
\(\widehat{BFH}=\widehat{CEH}=90^o\)
=> \(\Delta BHF\) s \(\Delta CHE\) (g - g)
b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{A}\) là góc chung
\(\widehat{AEB}=\widehat{AFC}=90^o\)
=> \(\Delta ABE\) s \(\Delta ACF\) (g - g)
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
=> AF . AB = AE . AC
c) Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{A}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\) (vì \(\Delta ABE\) s \(\Delta ACF\))
=> \(\Delta AEF\)s \(\Delta ABC\) (c - g - c)
d) Câu d mình không nghĩ ra. Bạn tự làm nha, chắc là xét tam giác đồng dạng rồi suy ra hai góc bằng nhau và sẽ suy ra đường phân giác đó.

a) Xét ΔABC có
BE là đường cao ứng với cạnh AC(gt)
CF là đường cao ứng với cạnh AB(gt)
BE cắt CF tại H(gt)
Do đó: H là trực tâm của ΔABC(Tính chất ba đường cao của tam giác)
Suy ra: AH⊥BC
b) Xét tứ giác BHCK có
HC//BK(gt)
BH//CK(gt)
Do đó: BHCK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: Hai đường chéo HK và BC cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà M là trung điểm của BC(gt)
nên M là trung điểm của HK
hay H,M,K thẳng hàng(đpcm)