Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/Có \(\frac{AM}{BM}=\frac{AN}{NC}=\frac{3}{4}\) Thales suy ra ĐPCM
b/Ta có \(\frac{MK}{BI}=\frac{AK}{AI}\left(1\right),\frac{NK}{IC}=\frac{AK}{AI}\left(2\right)\)
(1)=(2) mà BI=IC nên MK=NK
c/Vì MN//BC nên \(\frac{MK}{IC}=\frac{NK}{BI}\)
Ba đ/thẳng CM,BN,AI định lên 2 đ/thẳng MN//BC các cặp tỉ lệ bằng nhau nên chúng đồng quy tại 1 điểm
em hoc lop 7 nhung em nghi la phuong phap dong vi
Tức ghê á, gửi cái ảnh cũng không được, tôi làm vậy !!
A B C M N I O K
Tóm tắt :
Ta có :
\(\frac{MI}{BK}=\frac{MN}{BC}=\frac{AM}{AB}\) ( Talet ) . Rồi chứng minh hai tam giác đồng dạng AMI và ABK
\(\Rightarrow A,I,K\) thẳng hàng (1)
Lại có :
\(\frac{MI}{KC}=\frac{MN}{BC}=\frac{OM}{OC}\) ( Talet ). Rồi chứng minh hai tam giác đồng dạng MIO và CKO
\(\Rightarrow I,O,K\) thẳng hàng (2)
Từ (1) và (2) suy ra A,I,K,O thẳng hàng.
Bạn tham khảo, thay các điểm khác thôi còn bài toán vẫn giống nhé !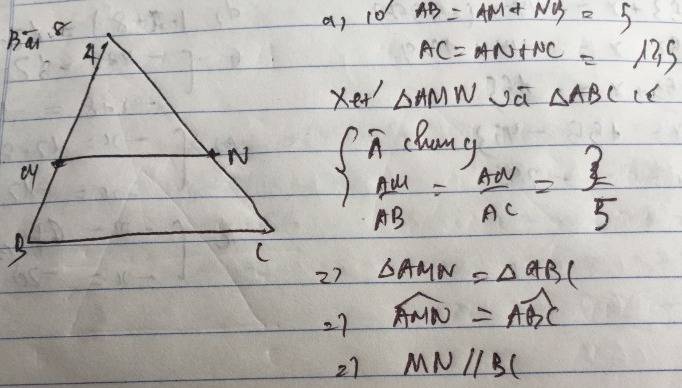
K đâu bạn?
có phải là I không?
AI cắt MN tại K
chứng minh I,O,K thẳng hàng