Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

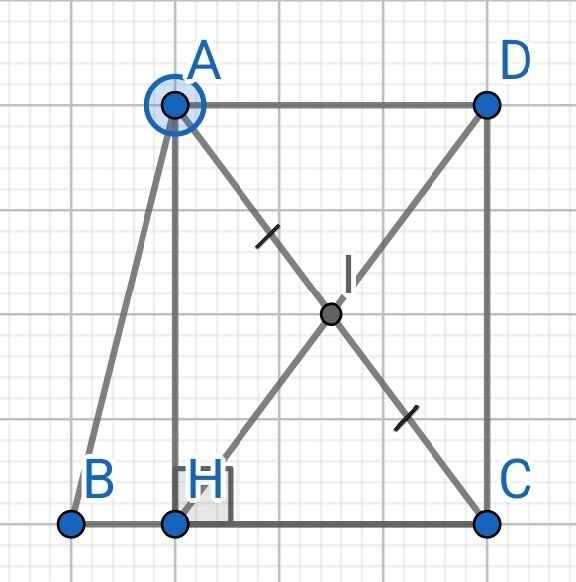
Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
Do đó: AHCD là hình bình hành
Hình bình hành AHCD có\(\widehat{AHC}=90^0\)
nen AHCD là hình chữ nhật

 Do D và H đối xứng nhau qua I (gt)
Do D và H đối xứng nhau qua I (gt)
⇒ I là trung điểm của DH
Do AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
⇒ ∠AHC = 90⁰
Tứ giác AHCD có:
I là trung điểm của AC (gt)
I là trung điểm của DH (cmt)
⇒ AHCD là hình bình hành
Mà ∠AHC = 90⁰ (cmt)
⇒ AHCD là hình chữ nhật

Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
+)Xét tứ giác AHCD có :
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
+)Hình bình hành AHCD có góc AHC = 90độ
=> AHCD là hình chữ nhật

Xét tứ giác AHCD có
M là trung điểm của AC
M là trung điểm của HD
Do đó: AHCD là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật

có:
M là trung điểm của AC (gt)
D đối xứng H qua M(gt) => M là trung điểm của DH
Xét tứ giác AHCD có:
2 đường chéo cắt nhau tại trung điểm mỗi đường(cmt)
=> Tứ giác AHCD là hình chữ nhật
Nhớ tick cho mình nha

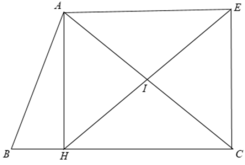
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có E A H ^ = A H C ^ = H C E ^ = C E A ^ = 90 0
⇒ AHCE là hình chữ nhật.

Xét tứ giác AHCD có
I là trung điểm chung của AC và HD
=>AHCD là hình bình hành
Hình bình hành AHCD có \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật