Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

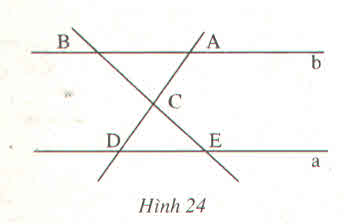
Ta có:
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.

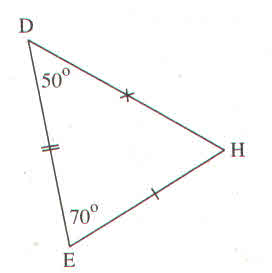
Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha

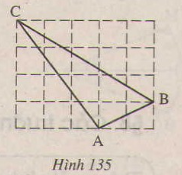
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
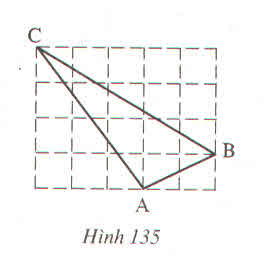
Giải:
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34

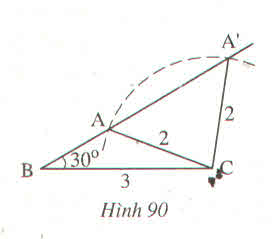
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.






Trả lời