Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tự vẽ hình:
Lấy F là trung điểm AC, K là điểm đối xứng với M qua F
Xét \(\Delta AMF\)và \(\Delta CKF\)có
FA=FC
FM=FK
,\(\widehat{AFM}=\widehat{CFK}\)
\(\Rightarrow\Delta AMF=\Delta CKF\left(c.g.c\right)\)
\(\Rightarrow CK=AM=BM\)(vì M là trung điểm AB)
Lại có:\(\widehat{FMA}=\widehat{FKC}\)
\(\Rightarrow\)AM//CK
\(\Rightarrow\widehat{KCM}=\widehat{BMC}\)
\(\Rightarrow\Delta BMC=\Delta KCM\left(c.gc\right)\)
\(\Rightarrow\widehat{CMK}=\widehat{MCB}\)
=>MK//BC
Mặt khác:MK=CB=>BC=2MF(vì F là TĐ MK)
\(\Rightarrow MK=\frac{1}{2}BC=BN+NC=CE\Rightarrow MF=CE\)
Vì MK//BC=>MF//CE=>\(\widehat{MFI}=\widehat{ICE},\widehat{FMI}=\widehat{IEC}\)
\(\Rightarrow\Delta MIF=\Delta EIC\left(g.c.g\right)\)
\(\Rightarrow IM=IE\)

Lên google cũng dc mà vừa nhanh vừa chính xác giống như tui vậy :)

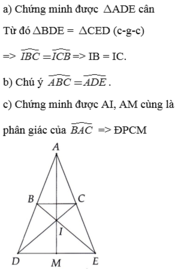
a, đơn giản ta CM được hai tam giác DCB và EBC bằng nhau => góc EBC = góc DCB => tam giác BIC cân tại I => IB = IC (đpcm)
tương tự chứng minh được hai tam giác DIB và EIC bằng nhau => ID = IE (đpcm)
b, ta có tam giác DAE cân tại A => 2góc D = 180o -góc A
tam giác BAC cân tại A => 2 góc B = 180o - góc A
=> góc D = góc B => BC// DE (đpcm)
c, Nối AM => AM vừa là trung tuyến vừa là đường trung trựctại M của BC
Nối IM => IM vừ là trung tuyến vừa là đường trung trực tại M của BC
=> AM và IM cùng nằm trên đường trung trực của BC tại M hay 3 điểm A,M,I thẳng hàng
a) Tam giác ABC cân tại A suy ra \(\widehat{B_1}=\widehat{C_1}\)
Xét tam giác ABM và tam giác ACM có :
AB = AC ( tam giác ABC cân tại A )
\(\widehat{B_1}=\widehat{C_1}\left(cmt\right)\)
BM = CM ( gt )
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ABI và tam giác ACI có :
AI chung
AB = AC ( tam giác ABC cân tại A )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c-g-c\right)\)
\(\Rightarrow IB=IC\)
Vì AD = AB + BD
AE = AC + BC
Mà AB = AC ( tam giác ABC cân tại A )
DB = EC ( gt )
\(\Rightarrow AD=AE\)
Xét tam giác ADI và tam giác AEI có :
AI chung
AD = AE ( cmt )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ADI=\Delta AEI\left(c-g-c\right)\)
\(\Rightarrow DI=EI\)hay ID = IE
b) Vì tam giác ABC cân tại A ( gt )
\(\Rightarrow\)\(\widehat{B_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì tam giác ADE có AD = AE ( cmt )
Suy ra tam giác ADE cân
\(\Rightarrow\widehat{D}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{B_1}=\widehat{D}\)mà hai góc này ở vị trí đồng vị
Suy ra BC // DE
c) Ta có : \(\widehat{M_2}=\widehat{M_1}\left(\Delta ABM=\Delta ACM\right)\left(cmt\right)\)
Mà \(\widehat{M_1}+\widehat{M_2}=180^o\)( 2 góc này ở vị trí kề bù )
\(\widehat{M_2}=\widehat{M_3}\)( đối đỉnh )
\(\Rightarrow\widehat{M_1}+\widehat{M_3}=180^o\)
\(\Rightarrow\)A ; M ; I thẳng hàng