Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác MAB và tam giác MDC có :
MB = MC do M là trđ của BC (gt)
MD = MA (GT)
góc BMA = góc DMC (Đối đỉnh)
=> tam giác MAB = tam giác MDC (c-g-c)
b, tam giác MAB = tam giác MDC (Câu a)
=> AB = DC (đn)
và góc BAM = góc MDC (đn) mà 2 góc này slt
=> AB // DC (Đl)
c, AB // DC (Câu b)
=> góc ABC = góc BCD (slt)
xét tam giác ABC và tam giác DCB có : BC chung
AB = DC (câu b)
=> tam giác ABC = tam giác DCB (c-g-c)
=> góc BAC = góc CDB (đn)

a) Xét \(\Delta MAB\)và \(\Delta MDC\)có:
MA = MD (gt)
\(\widehat{BMA}=\widehat{CMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c-g-c\right)\)
\(\Rightarrow AB=DC\)(2 cạnh tương ứng)
\(\widehat{BAM}=\widehat{CDM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
b) Xét \(\Delta ACM\)và \(\Delta DBM\)có:
MA = MD (gt)
\(\widehat{AMC}=\widehat{BMD}\)(2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\Delta ACM=\Delta DBM\left(c-g-c\right)\)
\(\Rightarrow AC=DB\)(2 cạnh tương ứng)
Xét \(\Delta BAC\)và \(\Delta CDB\)có:
AB = DC (cmt)
AC = DB (cmt)
BC là cạnh chung
\(\Rightarrow\Delta BAC=\Delta CDB\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{CDB}\)(2 góc tương ứng)
c) Bn tự lm nhá!! Phần này mk chưa nghĩ ra. Tốn chất xám lắm!!!!!

Hình tự vẽ nhé!
Bài giải:
c)Theo câu a ta có: Tam giác MAB=MDC=>Góc BAM=CDM.
Xét Tam giác AEM và DFM có:
AE=DF(GT)
Góc BAM=CDM (CMT)
AM=DM(GT)
=> Tam giác AEM=Tam giác DFM (c.g.c) => Góc AME=DMF(*)( góc tương ứng).
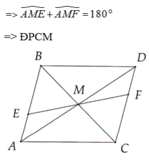
Mặt khác MA và MD là 2 tia đối nhau nên ta có:Góc AMF+DMF= 180 độ.
Từ (*) => Góc AMF+AME=180 độ =>ME và MF là hai tia đối nhau (theo dhnb) => E;M;F thẳng hàng(đpcm)

1 Xét 2 tam giác MAB và tam giác MDC:
Ta thấy:
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=MC (gt)
MA=MD (gt)
Từ các giả thiết trên, suy ra:
\(\Delta MAB=\Delta MDC\left(c-g-c\right)\)

sorry nhe ! minh moi hoc lop 6