Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
Qua $D$ vẽ đường thẳng song song với $OB$, cắt $AC$ tại $M$
Xét $\Delta ADM$ có $OK//DM$
$\Rightarrow \dfrac{AK}{KM}=\dfrac{OA}{OD}$ (định lí Ta-lét)
Nên $\dfrac{AK}{KM}=\dfrac{3}{2}$ (vì $\dfrac{OA}{OD}=\dfrac{3}{2}$)
Xét $\Delta BKC$ có $DM//BK$
$\Rightarrow \dfrac{KM}{CM}=\dfrac{DB}{DC}$ (định lí Ta-lét)
Nên $\dfrac{KM}{CM}=\dfrac{1}{2}$ (vì $\dfrac{DB}{DC}=\dfrac{1}{2}$) $\Rightarrow \dfrac{KM}{KM+CM}=\dfrac{1}{1+2} \Rightarrow \dfrac{KM}{KC}=\dfrac{1}{3}$
Do đó $\dfrac{AK}{KC}=\dfrac{AK}{KM}.\dfrac{KM}{KC}=\dfrac{3}{2}.\dfrac{1}{3}=\dfrac{1}{2}$

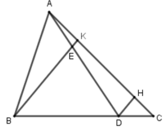
Qua D kẻ đường thẳng song song với BK cắt AC ở H.
Theo định lý Ta-lét:
Do EK // DH nên A K K H = A E E D = 1 2 (1)
Do DH //BK nên K H K C = B D B C = 3 4 (2)
Từ (1) và (2) suy ra A K K H . K H K C = 1 2 . 3 4 = 3 8
Vậy A K K C = 3 8
Đáp án: C

A B C E D I M N từ I kẻ IM vuông góc AC , từ B kẻ BN vuông góc AC => IM // BN
áp dụng định lý Menelous vào tam giác BCD có 3 điểm A ,I , E thẳng hàng và cắt 3 cạnh tam giác :
\(\dfrac{EC}{EB}\cdot\dfrac{IB}{ID}\cdot\dfrac{AD}{AC}=1\)
=> 2 . \(\dfrac{IB}{ID}\) . 3/4 = 1
=> \(\dfrac{IB}{ID}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{DI}{DB}=\dfrac{3}{7}\)
Do IM // BN => \(\dfrac{DI}{DB}=\dfrac{IM}{BN}=\dfrac{3}{7}\)
S abc = \(\dfrac{1}{2}BN\cdot AC\)
S iad = \(\dfrac{1}{2}IM\cdot AD\) \(\Rightarrow\dfrac{Siad}{Sabc}=\dfrac{IM}{BN}\cdot\dfrac{AD}{AC}=\dfrac{3}{7}\cdot\dfrac{3}{4}=\dfrac{9}{28}\)
mà S iad = 18 => S abc = 28*18 : 9 = 56


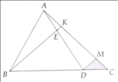
có sai đề ko zậy
chep y cuar co giao