Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M E N G
a) Ta có: AE = BE (gt)
AN = CN (gt)
BM = CM (gt)
mà AB = AC = BC (tam giác ABC đều)
\(\Rightarrow AE=BE=AN=CN=BM=CM\)(1)
Xét ba tam giác BAN, CAE và ACM ta có:
AB = AC (gt) (2)
góc BAC = góc ACM (gt) (3)
AE = AN = MC (gt) (4)
Từ (2),(3),(4) \(\Rightarrow\) ba tam giác BAN, CAE và ACM bằng nhau (5)
Từ (5) \(\Rightarrow\) AM = BN = CE (các cạnh tương ứng)
b) Xét các tam giác ABM, ACM, ABN, CBN, ACE, BCE ta có:
AB = AC = BC (gt) (6)
góc BAC = góc ABC = góc ACB (gt) (7)
AE = BE = AN = CN = BM = CM (1)
Từ (6),(7),(1) \(\Rightarrow\) các tam giác ABM, ACM, BAN, BCN, ACE, BCE bằng nhau (8)
Từ (8) \(\Rightarrow\) góc BAM = góc CAM = góc ABN = góc CBN = góc ACE = góc BCE
\(\Rightarrow\) góc CAM = góc ABN = góc BCE (9)
Từ (8) \(\Rightarrow\) góc AMB = góc AMC = góc BNA = góc BNC = góc AEC = góc BEC
\(\Rightarrow\) góc BNA = góc BEC = góc AMC (10)
Xét ba tam giác ANG, BEG, CMG ta có:
góc CAM = góc ABN = góc BCE (9)
AN = BE = MC (gt) (11)
góc BNA = góc BEC = góc AMC (10)
Từ (9),(11),(10) \(\Rightarrow\) ba tam giác ANG, BEG, CMG bằng nhau (12)
Từ (12) \(\Rightarrow\) GA = GB = GC (các cạnh tương ứng)
c) Xét ba tam giác AEN, BME, CMN ta có:
AN = BE = MC (gt) (11)
góc BAN = góc ABC = góc ACB (gt) (7)
AE = BM = CN (gt) (12)
Từ (11),(7),(12) \(\Rightarrow\) ba tam giác AEN, BME, CMN bằng nhau (13)
Từ (13) \(\Rightarrow ME=MN=EN\)(các cạnh tương ứng)
nên \(\Delta MNE\) là tam giác đều

mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên

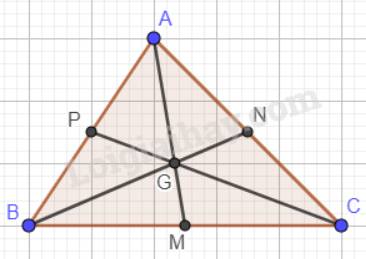
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).

Đề có sai không bạn , nếu `Delta ABC` là tam giác thường thôi thì không cm đc đâu ạ

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC

A B C G M P N
a) tg ABC đều
mà G là trọng tâm
=> AG,CG,BG là dg pg
thì có các tg AGB, AGC,BGC cân
=> AG=CG=BG
b) tg APN cân tại A(tự cm)
mà góc A(lớn ) = 60độ
=> tg APN đều => góc ANP=góc ACB
=>PN//BC(...)
CMT vs các tg MNC,PMB
c)tg MNC=tgPMB=tg PNA(M,N,P lần lượt là tđ của BC,AC,AB)
=> MN=PM=PN
=> tg PMN đều

Cho tam giác HPG có 3 trung tuyến HM,PA,GB cắt nhau tại T . Biết TH = 3 cm,TP=TG=4 cm a, Tính HM,PA,GB. b, Chứng minh tam giác HPG cân

A B C M N G
A)
Nhắc lại: -Trong 1 tam giác vuông bất kỳ, đường trung tuyến ứng với cạnh huyền của tam giác sẽ có độ dài bằng 1/2 cạnh huyền
Xét \(\Delta ABC\)vuông tại A
Có AM là trung tuyến
=> \(AM=\frac{1}{2}BC\left(đpcm\right)\)
b) Xét \(\Delta ABC\)vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\left(PYTAGO\right)\)
\(\Leftrightarrow BC^2=6^2+8^2\Leftrightarrow BC^2=100\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
Vì \(AM=\frac{1}{2}BC\)
\(\Leftrightarrow AM=\frac{1}{2}.100\Leftrightarrow AM=50\left(cm\right)\)
Ta có hai đường trung tuyến Am và BN cắt nhau tại G
=> G là trọng tâm tam giác ABC
\(\Rightarrow AG=\frac{2}{3}AM\)
\(\Leftrightarrow AG=\frac{2}{3}.50\Leftrightarrow AG\approx33,3\left(cm\right)\)
mình làm tiếp trang khác

a) Xét \(\text{∆}ABC\)vuông tại A
Vì AM là đường trung tuyến từ đỉnh A đến trung điểm cạnh huyền BC
=> \(AM=\frac{1}{2}BC\)(theo tính chất đường trung tuyến trong tam giác vuông) (đpcm)
b) Tính cạnh GA
Xét \(\text{∆}ABC\)vuông tại A
Theo định lí PYTAGO, ta có:
\(BC^2=AC^2+AB^2\)
\(BC^2=6^2+8^2\)
\(BC^2=36+64\)
\(BC^2=100\)
\(BC=\sqrt{100}=10\left(cm\right)\)
Mà \(AM=\frac{1}{2}BC\)nên:
\(AM=\frac{1}{2}BC=\frac{1}{2}.10=5\left(cm\right)\)
Vì BN và AM là hai đường trung tuyến nên G là trọng tâm của \(\Delta ABC\)
Ta có: \(GA=\frac{2}{3}AM\)nên:
\(GA=\frac{2}{3}AM=\frac{2}{3}.5\approx3,3\left(cm\right)\)
Tính cạnh GB:
Xét \(\text{∆}ABC\)vuông tại A, ta có:
BN là đường trung tuyến của \(\text{∆}ABC\)nên:
\(CN=NA\)
=> \(NA=\frac{1}{2}AC=\frac{1}{2}.4=2\left(cm\right)\)
Xét \(\text{∆}ANB\)vuông tại A
Theo định lý PYTAGO, ta có:
\(BN^2=NA^2+AB^2\)
\(BN^2=2^2+6^2\)
\(BN^2=4+36\)
\(BN^2=40\)
\(BN=\sqrt{40}\approx6,3\left(cm\right)\)
Ta lại có:
\(GB=\frac{2}{3}BN=\frac{2}{3}.6,3=4,2\left(cm\right)\)
Tính cạnh GC:
Trong \(\text{∆}ABC\), vẽ đường trung tuyến từ C xuống trung điểm của AB, gọi D là trung điểm của cạnh AB
Vì CD là đường trung tuyến của \(\text{∆}ABC\)nên:
\(AD=DB\)
=> \(AD=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
Xét \(\text{∆}CAD\)vuông tại A
Theo định lí PYTAGO, ta có:
\(CD^2=AC^2+AD^2\)
\(CD^2=8^2+3^2\)
\(CD^2=64+9\)
\(CD^2=73\)
\(CD=\sqrt{73}=8,5\left(cm\right)\)
Ta lại có:
\(GC=\frac{2}{3}CD=\frac{2}{3}.8,5\approx5,7\left(cm\right)\)


a:
Ta có: ΔBCA đều
=>AB=BC=AC và \(\widehat{ABC}=\widehat{BAC}=\widehat{ACB}=60^0\)
Xét ΔEBC vuông tại E và ΔNCB vuông tại N có
BC chung
\(\widehat{EBC}=\widehat{NCB}\)
Do đó: ΔEBC=ΔNCB
=>\(\widehat{GBC}=\widehat{GCB}\)
=>ΔGBC cân tại G
=>GB=GC
Xét ΔMCA vuông tại M và ΔEAC vuông tại E có
AC chung
\(\widehat{MCA}=\widehat{EAC}\)(=60 độ)
Do đó: ΔMCA=ΔEAC
=>\(\widehat{GCA}=\widehat{GAC}\)
=>GA=GC
=>GB=GC=GB
b: ΔBAC đều
mà AM là đường cao
nên M là trung điểm của BC
ΔBAC đều
mà BN là đường cao
nên N là trung điểm của AC
ΔABC đều
mà CE là đường cao
nên E là trung điểm của AB
Xét ΔABC có
AM,BN,CE là các đường trung tuyến
AM,BN,CE đồng quy tại G
Do đó: G là trọng tâm của ΔABC
c: Ta có: ΔBEC=ΔCNB
=>EC=NB
ΔEAC=ΔMCA
=>EC=MA
=>AM=BN=CE
♬⚽