Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình có cách này bạn xem thử và check nhé!
Do tam giác ABC có \(\widehat{A}=\widehat{B}+\widehat{C}\). Mà tổng ba góc trong tam giác là 180o nên \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Leftrightarrow\widehat{A}+\widehat{A}=180^o\Leftrightarrow2.\widehat{A}=180^o\Leftrightarrow\widehat{A}=90^o=\widehat{B}+\widehat{C}\). Do đó tam giác ABC vuông tại A.
A B C O 1 2 1 2
Ta có: Xét tam giác ABC,theo định lí về tổng số đo của ba góc trong tam giác,ta suy ra
\(\widehat{BOC}=180^o-\left(\widehat{B_1}+\widehat{C_1}\right)\) (1)
\(=180^o-\left(\widehat{B}+\widehat{C}-\widehat{B_2}-\widehat{C_2}\right)=180^o-90^o+\widehat{B_2}+\widehat{C_2}=90^o+\widehat{B_2}+\widehat{C_2}=90^o+\widehat{B_1}+\widehat{C_1}\) (2) (do \(\widehat{B_1}=\widehat{B_2};\widehat{C_1}=\widehat{C_2}\)).Từ (1) và (2),ta có: \(180^o-\left(\widehat{B_1}+\widehat{C_1}\right)=90^o+\widehat{B_1}+\widehat{C_1}\Rightarrow180^o-90^o=2\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=45^o\). Thay vào (1) (hoặc thay vào (2) cũng được) ,ta suy ra: \(\widehat{BOC}=180^o-\left(\widehat{B_1}+\widehat{C_1}\right)=180^o-45=135^o\)

`hatA+hatB+hatC=180^o`
mà `hatA=hatB+hatC `
`=>hatA+hatA=180^o`
`=>2hatA=180^o`
`=>hatA=90^o`
`+)hat{BOC}=180- (hat{OBC}+hat{OCB})`
.vì o là giao điểm của 3 đường phân giác
`=>2(hat{BOC}+hat{OCB})=hatA=90^o`
`=>hat{BOC}=180^o-90^o/2=180^o-45^o=135^o`

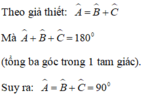
Do AO, CO lần lượt là tia phân giác của ∠A và ∠C nên BO là tia phân giác của ∠B
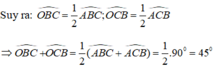
Xét tam giác OBC có:
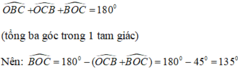
Chọn (C) 135º.

Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!