Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Xét △ABC có: E thuộc AB, D thuộc BC, H thuộc AC và AD, BH, CE đồng quy tại I.
\(\Rightarrow\dfrac{AH}{HC}.\dfrac{DC}{DB}.\dfrac{EB}{EA}=1\) (định lí Ceva).
\(\Rightarrow\dfrac{AH}{HC}.\dfrac{DC}{DB}=1\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{DB}{DC}\Rightarrow\)HD//AB.
\(\Rightarrow S_{ABD}=S_{ABH}\Rightarrow S_{ABD}-S_{ABI}=S_{ABH}-S_{ABI}\Rightarrow S_{IBD}=S_{AIH}\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Sửa đề: Đường trung tuyến CM của ΔABC cắt HD tại N
Ta có: HD\(\perp\)AC
AB\(\perp\)AC
Do đó: HD//AB
=>ND//AM và HN//MB
Xét ΔCAM có ND//AM
nên \(\dfrac{ND}{AM}=\dfrac{CN}{CM}\left(1\right)\)
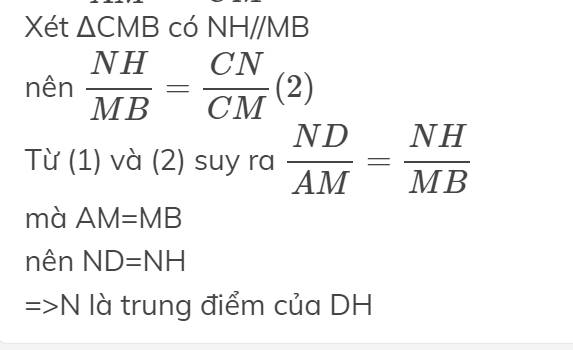
Xét ΔCMB có NH//MB
nên \(\dfrac{NH}{MB}=\dfrac{CN}{CM}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{ND}{AM}=\dfrac{NH}{MB}\)
mà AM=MB
nên ND=NH
=>N là trung điểm của DH

ΔAHE vuông tại H nên AH<AE
=>góc AEH<90 độ
=>góc AED>90 độ
=>AE<AD
=>AH<AE<AD

-Xét △ABC có: H∈AC, D∈BC, E∈AB ; AD, BH, CE đồng quy
\(\Rightarrow\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{HC}{HA}=1\) (định lí Ceva)
\(\Rightarrow\dfrac{DB}{DC}.\dfrac{HC}{HA}=1\Rightarrow\dfrac{HA}{HC}=\dfrac{DB}{DC}\)
\(\Rightarrow\)HD//AB (định lí Ta-let đảo)