Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

) HS tự chứng minh AMBQ là hình chữ nhật (ahi đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
b) Sử dụng tính chất trực tâm tam giác.
c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh
P I = P Q = 1 2 A B .

a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)(hai góc so le trong, BM//AC)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)(hai góc đối đỉnh)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
=>P là trung điểm của MQ
Xét tứ giác AMBQ có
P là trung điểm chung của AB và MQ
=>AMBQ là hình bình hành
Hình bình hành AMBQ có \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
b: Ta có: AMBQ là hình chữ nhật
=>BQ\(\perp\)AQ tại Q
=>BQ\(\perp\)AC tại Q
Xét ΔABC có
BQ,AI là các đường cao
BQ cắt AI tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
c: Ta có: AMBQ là hình chữ nhật
=>AB=QM
mà \(PQ=\dfrac{QM}{2}\)
nên \(PQ=\dfrac{AB}{2}=PA\)(1)
Ta có: ΔAIB vuông tại I
mà IP là đường trung tuyến
nên IP=PA(2)
Từ (1) và (2) suy ra PI=PQ
=>ΔPIQ cân tại P

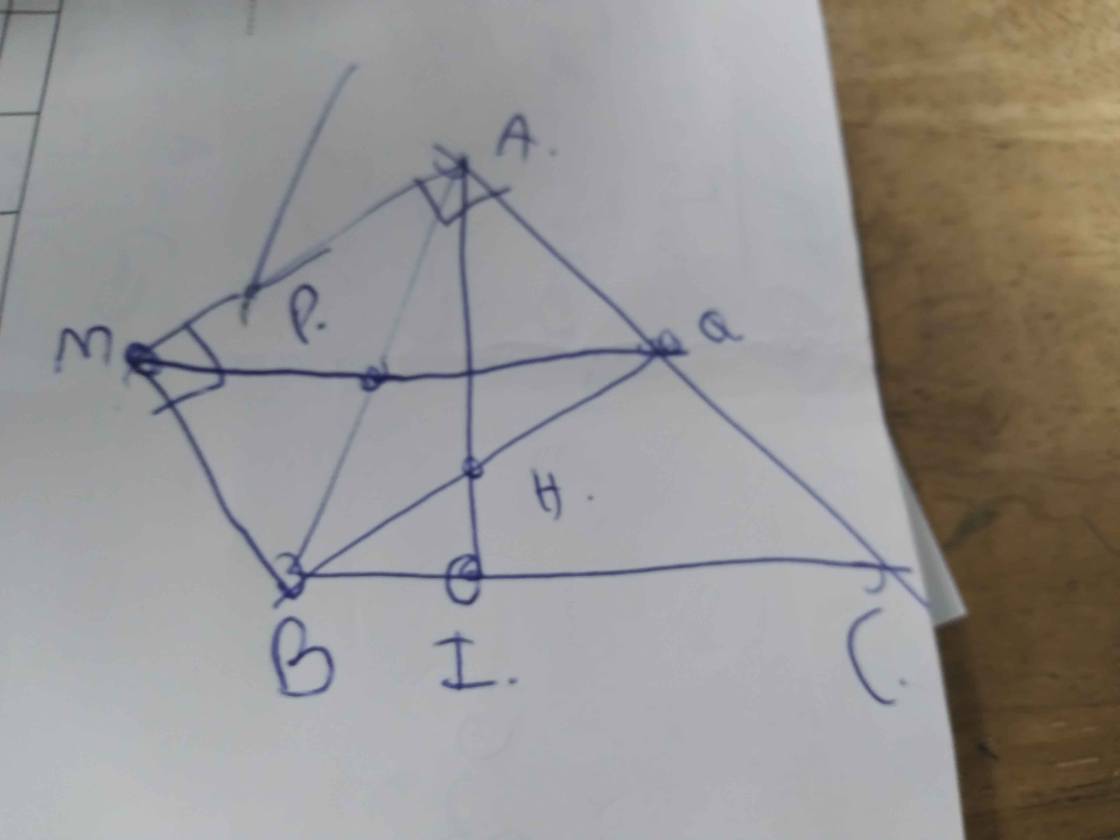
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
Suy ra: MB=AQ
Xét tứ giác AMBQ có
MB//AQ
MB=AQ
Do đó: AMBQ là hình bình hành
mà \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
Câu a có r mk ko ghi lại nx nhe
b) Ta có AQBM là HCN (CMa)
=> ^AQB=900 hay BQ ⊥ AC
=> BQ là đường cao của ΔABC
Mà H là giao điểm của 2 đường cao AI và BQ của ΔABC (gt)
=> H là trực tâm của ΔABC
=> CH cũng là đường cao của ΔABC (H là trực tâm; H ∈ CH)
=> CH ⊥ AB (đpcm)