Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

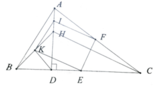
a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông

câu hỏi hay......nhưng tui xin nhường cho các bn khác
Hãy tích đúng cho tui nha
THANKS

a/
+ Xét tg AHB có
IA=IH (đề bài)
KB=KH (đề bài)
=> IK là đường trung bình của tg ABH => IK//=AB/2 (1)
+ Xét tam giác ABC có
FA=FC (đề bài)
EB=EC (đề bài)
=> EF là đường trung bình của tg ABC => EF//=AB/2 (2)
Từ (1) và (2) => Tứ giác KIFE là hình bình hành) (3)
+ Xét tam giác BHC có
KB=KH
EB=EC
=> KE là đường trung bình của tg BHC => KE//HC
mà HC vuông góc với AB (H là trực tâm)
=> KE vuông góc với AB
Ta đã c/m ở trên là IK//AB
=> IK vuông góc với KE (4)
Từ (3) và (4) => KIFE là hình chữ nhật (hình bình hành có 1 góc vuông là HCN)
+ Ta có K và F cùng nhìn IE dưới 1 góc vuông => K; F nằm trên đường tròn đường kings IE => E; F; I; K cùng nằm trên 1 đường tròn đường kính IE
b/ Ta có AD vuông góc BC => D cũng nhìn IE dưới 1 góc vuông => D thuộc đường tròn đường kính IE

a) Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BFC};\widehat{BEC}\) là các góc cùng nhìn cạnh BC
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)