Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
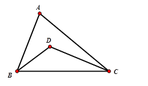
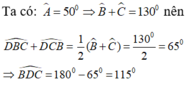
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC

Chọn đáp án D
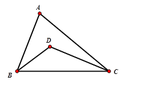
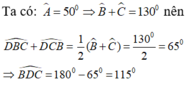
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC

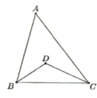
Ta có A ^ = 50 0 ⇒ B ^ + C ^ = 130 0
D B C ^ + D C B ^ = 65 0 ⇒ B D C ^ = 115 0
=> Quỹ tích của điểm D là hai cung chứa góc 115 0 dựng trên đoạn BC

*Chứng minh thuận:
Gọi I là giao điểm của ba đường phân giác trong của tam giác ABC



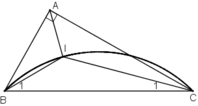
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135 º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135 º dựng trên đoạn BC.
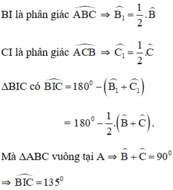
⇒ I thuộc cung chứa góc 135 º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135 º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135 º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của 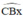
+ Kẻ tia Cy sao cho CI là phân giác của 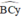
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
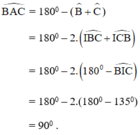
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135 º dựng trên đoạn BC (khác B và C).
Kiến thức áp dụng
+ Thông thường, bài toán quỹ tích ta làm theo các bước :
1, Dự đoán quỹ tích
2, Chứng minh quỹ tích : gồm Phần thuận và Phần đảo
3, Kết luận.
+ Quỹ tích các điểm M thỏa mãn 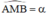 (với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).
(với A, B cố định, α không đổi) là cung chứa góc α dựng trên đoạn AB. (Cách dựng xem SGK).

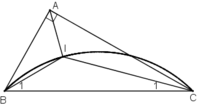
* Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
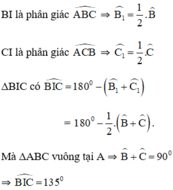
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC
+ Kẻ tia Bx sao cho BI là phân giác của 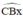
+ Kẻ tia Cy sao cho CI là phân giác của 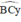
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC
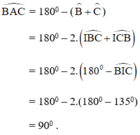
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận : Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).

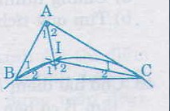
Theo tính chất của góc ngoài tam giác, ta có;
\(\widehat{I_2}=\widehat{A_1}+\widehat{B_1}\) (1)
\(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\) (2)
Cộng vế (1) và (2) vế với vế:
\(\widehat{I_1}+\widehat{I_2}=\widehat{A_1}+\widehat{A_2}+\widehat{B_1}+\widehat{C_1}\)
Hay \(\widehat{I}=90^o+45^o=135^o\)
Điểm I nhìn đoạn thẳng BC cố định dưới góc 135o không đổi, vậy quỹ tích của I là góc cung chứa góc 135o dựng trên đoạn thẳng BC
Một CTV gương mẫu chưa từng thấy! :)
Vậy mà cũng là CTV học tập! :)

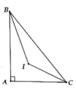
Tương tự câu 1
Tính được B I C ^ = 135 0
=> Quỹ tích của điểm I là hai cung chứa góc 135 0 dựng trên đoạn BC
