Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
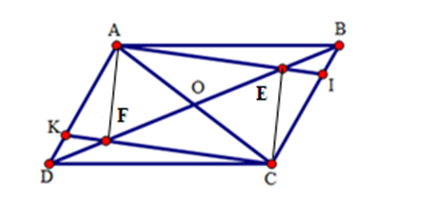
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Bài 6:
Xét ΔADE vuông tại D và ΔDCF vuông tại C co
AD=DC
DE=CF
Do đó: ΔADE=ΔDCF
=>AE=DF và góc AED=góc DFC
=>góc AED+góc FDC=90 độ
=>DF vuông góc với AE

(Đề là trên tia BC nha)
â) Xét tam giác ABM va tam giac ADN ( ABM = ADN=90) , co :
BM=DN(gt)
AD=AB(ABCD là hinh vuông)
=> tam giac ABM = tam giac ADN (cgv-cgv)
=>AN=AM va MAB = NAD
Ta co : MAB + DAM=90
Ma MAB =NAD (cmt)
=>NAD + DAM =90
<=> NAM =90
Xet tg ANFM , co : AN//FM (gt) va AM//NF (gt)
=> ANFM la hbh
Ma NAM =90 (cmt) ; AN=AM (cmt)
=> ANFM là hình vuông ( Vì đây là hình chữ nhật có 2 cạnh kề bằng nhau )
b) Từ F kẻ FP vuông góc với NC , FH vuông góc với BC
Xét tam giác NPF và tam giác MHF (APF =HMF) , co :
MF = FN (AMFN la hinh vuong )
NFP=MFH ( cùng phụ với PFM )
=> tam giác NPF = tam giác MHF (c.huyen-gn)
=> PF=FH
Theo định lý đảo của tia phân giác trong NCM , co :
PF=FH(cmt)
Ma PF \(\perp\) PC (cách ve ) ; FH \(\perp\) CH
=> F nằm trên tia phân giác của NCM
c)Nói C và F , ta được CF là tia phân giác của NCM (câu b)
Ta có : PCF + FCH =PCH =90
Mà PCF = FCH ( CF là tia phân giác NCM)
=> PCH = 2 PCF (1)
Ta co : ACD + ACB = DCB =90
Mà ACD = ACB ( AC là tia phân giác DCB ; ABCD là hình vuông )
=> DCB = 2 ACD (2)
Từ (1) vả (2) => PCH + DCB = 2( PCF + ACD)
<=> 180 = 2 ( PCF + ACD)
<=> 180 = 2 . ACF
<=> ACF = 90
=>AC \(\perp\) CF( dpcm )
đ) Gọi R là giao điểm của hai đường chéo tg ABCD là AC và BD
Xét tam giác AFC , co :
OA =OF ( gt)
AR = CR ( do 2 đường chéo AC và BD cắt nhau tại trung điểm mỗi đường trong hình vuông ABCD )
=> OR là đường trung bình của tam giác AFC
=> O và R cùng thuộc 1 đường thẳng
Mặt khác , ta có : R \(\in\) BD ( cach ve )
=> O \(\in\) BD
=> O , B, D thẳng hàng
Ta có : OB //FC ( OR là đường trung bình )
=> BOFC là hình thang

giúp mình vs, mình đang cần gấp ạ !!!