Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

D A E B C
Ta có : \(\widehat{DAB}=\widehat{CAE}=90^0\Rightarrow\widehat{DAB}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
hay \(\widehat{DAC}=\widehat{EAB}\)
Xét \(\Delta ADC\)và \(\Delta ABE\)có :
AD = AB
\(\widehat{DAC}=\widehat{EAB}\)
AC = AE
\(\Rightarrow\Delta ADC=\Delta ABE\left(c.g.c\right)\Rightarrow DC=BE\)
Vì tam giác ADC = tam giác ABE nên \(\widehat{AEB}=\widehat{ACD}\)
mà \(\widehat{AKE}=\widehat{BKC}\left(doi-dinh\right),\widehat{AKE}+\widehat{AEB}=90^0\)
\(\Rightarrow\widehat{BKC}+\widehat{AEB}=90^0\) hay góc \(\widehat{BKC}+\widehat{ACD}=90^0\)
\(\Rightarrow DC\perp BE\)

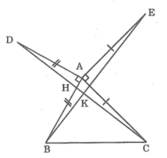
∠DAC = ∠DAB + ∠BAC = 90o + ∠BAC
∠BAE = ∠BAC + ∠CAE = ∠BAC + 90o
⇒ ∠DAC = ∠BAE
Xét ΔABE và ΔADC, ta có:


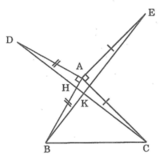
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)

Ta có: \(\widehat{DAC}=\widehat{DAB}+\widehat{BAC;}\widehat{BAE}=\widehat{EAC}+\widehat{BAC}.\)
Mà \(\widehat{DAB}=\widehat{EAC}\left(90^o\right);\widehat{BAC}chung.\)
\(\Rightarrow\) \(\widehat{DAC}=\widehat{BAE}.\)
Xét tam giác DAC và tam giác BAE:
+ AD = AB (gt).
+ AC = AE (gt).
+ \(\widehat{DAC}=\widehat{BAE}\left(cmt\right).\)
\(\Rightarrow\) Tam giác DAC = Tam giác BAE (c - g - c).
\(\Rightarrow\) DC = BE (2 cạnh tương ứng).