Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
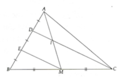

a) Xét ΔBCD có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//CD và \(ME=\dfrac{CD}{2}\)(Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
c) Xét ΔAEM có
D là trung điểm của AE
I là trung điểm của AM
Do đó: DI là đường trung bình của ΔAEM
Suy ra: DI//EM và \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: \(DI=\dfrac{EM}{2}\)(cmt)
nên \(EM=2\cdot DI\)
\(\Leftrightarrow\dfrac{DC}{2}=2\cdot DI\)
\(\Leftrightarrow DC=4\cdot DI\)
\(\Leftrightarrow DC-DI=4DI-DI\)
\(\Leftrightarrow CI=3DI\)


Do ME là đường trung bình của tam giác BDC nên \(ME//DC\)
Mặt khác I là trung điểm của AM;\(DI//EM\Rightarrow DE=DA\)
Mà \(ME=ED\) vì E trung điểm.
Vậy \(AD=DE=EB\)
Bổ sung chút cho bài của bạn Cood Kid
Gọi E là trung điểm BD
Xét tam giác BCD có M là trung điểm BC, E là trung điểm BD
=> ME là đường trung bình của tam giác BCD.

Vì \(AM\) là đường trung tuyến ứng với \(BC\left(gt\right)\)
=> \(MA=MB.\)
a) Nối \(E\) với \(M.\)
Xét \(\Delta BDC\) có:
\(\left\{{}\begin{matrix}DE=EB\left(gt\right)\\MA=MB\left(cmt\right)\end{matrix}\right.\)
=> \(ME\) là đường trung bình của \(\Delta BDC.\)
=> \(ME\) // \(CD\) (tính chất đường trung bình của tam giác)
Mà \(I\in CD\left(gt\right)\)
=> \(ME\) // \(ID.\)
Xét \(\Delta AEM\) có:
\(AD=AE\left(gt\right)\)
\(ME\) // \(ID\left(cmt\right)\)
=> \(I\) là trung điểm của \(AM\) (định lí đường trung bình của tam giác)
Chúc bạn học tốt!

a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.