Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC, các đường trung tuyến BD, CE và BC = 8cm
a) Chứng minh rằng: Tứ giác BEDC là hình thang.
b) Gọi M, N theo thứ tự là trung điểm của BE, CD. Tính MN?
c) Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh rằng:
giúp cái

A B C D E M N I K
Xin lỗi vì hình không được chính xác cho lắm.
a) Dễ thấy DE là đường trung bình nên DE // BC => Tứ giác BCDE là hình thang
b) Dễ thấy MN là đường trung bình do đó MN // ED (và BC nữa nhưng ở đây ko cần:v)
Ta có MN // ED -> MI // ED (1) . Mà M là trung điểm BE(2) . Từ (1) và (2) có ngay I là trung điểm BD.
Chứng minh tương tự (bạn tự chứng minh nhá) ta cũng có K là trung điểm CE.
c) Từ câu b) ta suy ra MI là đường trung bình nên \(MI=\frac{1}{2}ED\)
Tương tự \(KN=\frac{1}{2}ED\). Bây giờ phải chứng minh \(IK=\frac{1}{2}ED\) là xong . Tuy nhiên mình chưa nghĩ ra.
Làm tiếp:
c)Dễ thấy MK là đường trung bình (do từ câu b thì K là trung điểm EC)
Do đó \(MK=\frac{1}{2}BC\Leftrightarrow MI+IK=\frac{1}{2}BC\)
\(\Rightarrow IK=\frac{1}{2}BC-MI=\frac{1}{2}BC-\frac{1}{2}ED=\frac{1}{2}ED\) (do \(ED=\frac{1}{2}BC\))
Từ đây ta có thể suy ra đpcm.

A C B E D I K M N
Hình trên, đặt BC = a
Vì \(\Delta ABC\)có \(AE=EB;AD=DC\)nên \(ED\)là đường trung bình . Do đó ED song song BC và \(ED=\frac{BC}{2}=\frac{a}{2}\)
Do MN là đường trung bình của hình thang BEDC nên MN song song ED song song BC
\(\Delta BED\)có \(BM=ME;MI\)song song \(ED\)nên \(MI\)là đường trung bình , \(MI=\frac{ED}{2}=\frac{a}{4}\)
\(\Delta CED\)có \(CN=ND;NK\)song song \(ED\)nên \(NK\)là đường trung bình ,\(NK=\frac{ED}{2}=\frac{a}{4}\)
\(\Delta EBC\)có \(EM=MB;MK\)song song \(BC\)nên \(MK\)là đường trung bình ,\(MK=\frac{BC}{2}=\frac{a}{2}\)
\(\Rightarrow IK=MK-MI=\frac{a}{2}-\frac{a}{4}=\frac{a}{4}\)
Vậy \(MI=IK=KN\)

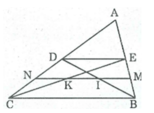
Trong ∆ ABC ta có: E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
⇒ ED // BC và ED = 1/2 BC
(tính chất đường trung bình của tam giác)
+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE
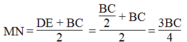
(tính chất đường trung bình hình thang)
Trong ∆ BED, ta có: M là trung điểm BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
⇒ MI = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
Trong ∆ CED ta có: N là trung điểm CD
NK // DE
Suy ra: NK là đường trung bình của ∆ CED
⇒ NK = 1/2 DE = 1/4 BC (tính chất đường trung bình của tam giác)
IK = MN – (MI + NK) = 3/4 BC – (1/4 BC + 1/4 BC) = 1/4 BC
⇒ MI = IK = KN = 1/4 BC

sao N đã là trung điểm CE mà MN còn cắt CE tại K nữa?
Gọi M và N theo thứ tự là trung điểm của BE và CD nhé , mình viết nhầm thành CE

A B C E D M N I K
Xét tg ABC có: E là t/đ của AB (gt) và D là t/đ của AC (gt)
=> DE là đg trung bình của tg ABC => ED = 1/2. BC ; ED//BC
Xét hthang EDCB(ED//BC) có: M là t/đ của BE (gt) và N là t/đ của DC(gt)
=> MN là đg trung bình của hthang EDCB => MN//DE//BC ; MN = 1/2.(DE+BC) . MÀ DE=1/2.BC (cmt)=> MN=3/2 . DE
=> MI+IK+KN =3/2 . DE (1)
xét tg BDE có: M là t/đ của BE(gt) ; MI//ED ( vì I thuộc MN ; MN//DE) => I là r/đ của BD => MI là đg trung bình của tg BDE
=> MI =1/2.DE (2)
C/m tương tự ta đc: KN là đg trung bình của tg CDE => KN= 1/2.DE (3)
Từ (2) ,(3)=> MI=KN =1/2.DE (*)
Thay (2),(3) vào (1) ta đc: 1/2. DE +IK +1/2. DE =3/2. DE => IK =1/2. DE (**)
Từ (*),(**)=> MI=IK=KN (đpcm)
Bạn có thể giải thích cho mình vì sao = 1/2.(DE+BC)Mà DE = 1/2BC => MN =3/2 là sao vậy mình không hiểu đoạn đó
nvbmmnlpoiwqvnaqw 098176235