K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

14 tháng 2 2020
Cho AH là trung tuyến tgiac ABC, AH cắt MN tại O
Có \(\frac{AM}{AB}=\frac{10}{15}=\frac{2}{3},\frac{AN}{AC}=\frac{14}{21}=\frac{2}{3}\)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{2}{3}\Rightarrow\) MN//BC
Xét \(\Delta ABH\) có MO//BH \(\Rightarrow\frac{AM}{AB}=\frac{AO}{AH}=\frac{2}{3}\Rightarrow\) O là trọng tâm tgiac ABC đc MN đi qua

2 tháng 5 2021
a, theo pitago đảo: 212 +282=1225=352 suy ra tam giác ABC vuông
b,theo pitago
AH2=AB2-BH2=AC2-CH2 suy ra 2AH2=AB2+AC2-BH2-CH2
suy ra 2AH2=BC2-BH2-CH2 (Mà BC=BH+CH) suy ra 2AH2=2BHxCH

15 tháng 3 2022
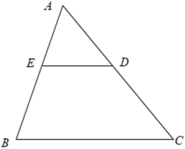
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC
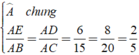
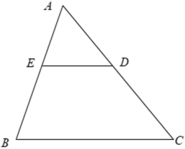
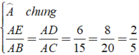
Xét \(\Delta\)AMN và \(\Delta\)ABC có:
\(\frac{AM}{AB}=\frac{AN}{AC}\left(\frac{10}{15}=\frac{14}{21}\right)\)
=> MN // BC (1)
Gọi M là trung điểm của BC.
Gọi G là giao điểm AM và MN
Xét \(\Delta\)ABM có:
MG// BM ( theo(1))
=> \(\frac{AG}{AM}=\frac{AM}{AB}=\frac{10}{15}=\frac{2}{3}\)
=> G là trọng tâm của \(\Delta\)ABC
Vậy MN qua trong tâm \(\Delta\)ABC.