Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

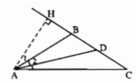
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)
Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º
+) Xét tam giác AHB vuông tại H ta có:
∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)
Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º
+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)
Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên
∠(BAC) = (180º − 112º) : 2 = 34o
+) Do AD là tia phân giác của góc BAC nên
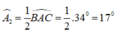
+ Từ đó
∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.
Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º
Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º

a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{CAD}=\widehat{HAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
Xét ΔABD có \(\widehat{BAD}=\widehat{BDA}\)
nên ΔBAD cân tại B
c: Xét ΔHDK vuông tại H và ΔEDC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)
Do đó: ΔHDK=ΔEDC

A B C H D
-Do Ad là tia phân gaisc của \(\widehat{A}\) nên \(\widehat{BAD}\)\(=\widehat{CAD}\)= \(45^o\)
=> \(\widehat{BAH}\)\(=\widehat{BAD}-\widehat{HAD}=45^o-15^o=30^o\)
-Xét tam giác ABH vuông tại H có: \(\widehat{B}=90^o-\widehat{BAH}=90^o-30^o=65^o\)
-Xét tam giác ABC vuông tại A có: \(\widehat{C}=90^o-\widehat{B}=90^o-65^o=25^o\)
Vậy \(\widehat{B}=65^o\), \(\widehat{C}=25^o\)

https://olm.vn/thanhvien/kaito1412tv
Bạn vào đây là có nhé

a) Tam giác ABC cân tại A, đường cao AH => H là trung điểm BC.
Xét tam giác BEC có HF song song với BE và đi qua trung điểm BC nên HF = 1/2 BE (ở đây chứng minh hơi cực, bạn tham khảo bài 63 và 64 trang 146 SBT Toán 7 tập một).
Kết hợp với giả thiết => tam giác AHF cân tại H.
b) Ta có ^EBH = ^FHC (do HF // BE), ^EBH = 1/2 ^ABC (BE là tia phân giác ^ABC) và ^ABC = ^HCF (tam giác ABC cân tại A) => ^FHC = 1/2 ^HCF.
c) Ta có ^HFA là góc ngoài tại đỉnh F của tam giác HFC nên ^HFA = ^FHC + ^HCF.
Kết hợp tam giác AHF cân tại H => ^HAC = ^FHC + ^HCF = 1/2 ^HCF + ^HCF = 3/2 ^HCF.
Tam giác AHC vuông tại H => ^HAC + ^HCF = 90 độ hay 3/2 ^HCF + ^HCF = 90 độ => ^HCF = 36 độ.
Từ đây bạn tính các góc còn lại.

( bạn tự vẽ hình)
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
a, xét tam giác ABE và tam giác ACE có:
AE chung
AB=AC (gt)
góc BAE=góc CAE( vì AE là tia phân giác của góc BAC)
=> tam giác ABE=tam giác ACE
b, vì tam giác ABE=tam giác ACE( cmt)=> BE=CE( 2 cạnh tương ứng)(1)
=> góc BEA=góc CEA ( 2 góc tương ứng)
mà 2 góc này kề bù
=> góc BEA=góc CEA= 180 độ : 2= 90 độ
=> AE vuông góc với BC (2)
từ (1) và (2) ta có AE là đường trung trực của BC.
\(\widehat{ABH}=180^0-112^0=68^0\)
Xét ΔAHB vuông tại H có
\(\widehat{ABH}+\widehat{BAH}=90^0\)
nên \(\widehat{BAH}=22^0\)
Vì ΔABC cân tại B
nên \(\widehat{BAC}=\dfrac{180^0-112^0}{2}=34^0\)
mà AD là phân giác
nên \(\widehat{BAD}=17^0\)
=>\(\widehat{HAD}=39^0\)
hay \(\widehat{HDA}=51^0\)