Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

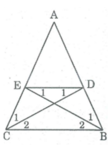
AD = AE (gt)
⇒ ∆ ADE cân tại A ⇒ ∠ (ADE) = ( 180 0 - ∠ A )/2
∆ ABC cân tại A ⇒ ∠ (ABC) = ( 180 0 - ∠ A )/2
Suy ra: ∠ (ADE) = ∠ (ABC)
⇒ DE // BC (Vì có cặp góc đồng vị bằng nhau)
Tứ giác BDEC là hình thang
∠ (ABC) = ∠ (ACB) (tính chất tam giác cân) hay ∠ (DBC) = ∠ (ECB)
Vậy BDEC là hình thang cân.

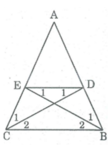
Ta có: BD = DE ⇒ ∆ BDE cân tại D
∠ B 1 = ∠ E 1
Mà ∠ E 1 = ∠ B 2 (so le trong)
⇒ ∠ B 1 = ∠ B 2
DE = EC ⇒ ∆ DEC cân tại E
⇒ ∠ D 1 = ∠ C 1
∠ D 1 = ∠ C 2 (so le trong)
⇒ ∠ C 1 = ∠ C 2
Vậy khi BE là tia phân giác của ∠ (ABC) , CD là tia phân giác của ∠ (ACB) thì BD = DE = EC

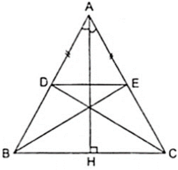
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.
Đề yêu cầu sao vậy bạn
đúng đúng