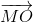Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))

Bài này có nhiều cách làm, vẽ thêm đường phụ cũng được, dùng định lý Menelaus cũng được nhưng lớp 10 thì nên dùng vecto
Ta có:
\(k=\dfrac{AG}{AB}=1-\dfrac{BG}{AB}=1-\dfrac{DE}{AB}=1-\dfrac{2DE}{3EF}\)
Đặt \(\dfrac{AD}{AM}=m\)
\(\Rightarrow\overrightarrow{ED}=m\overrightarrow{EM}+\left(1-m\right)\overrightarrow{EA}\)
\(=m\left(\overrightarrow{EC}+\overrightarrow{CM}\right)+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\dfrac{2}{3}m\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}+\dfrac{1}{3}\left(m-1\right)\overrightarrow{AC}\)
\(=\left(m-\dfrac{1}{3}\right)\overrightarrow{AC}+\dfrac{1}{2}m\overrightarrow{CB}\)
Lại có: \(\overrightarrow{EF}=\dfrac{2}{3}\overrightarrow{AB}=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{CB}\)
Mà \(D,E,F\) thẳng hàng nên:
\(\left(m-\dfrac{1}{3}\right)\dfrac{2}{3}=\dfrac{1}{2}m.\dfrac{2}{3}\Leftrightarrow m=\dfrac{2}{3}\)
\(\Rightarrow\overrightarrow{ED}=\dfrac{1}{2}\overrightarrow{EF}\Rightarrow ED=\dfrac{1}{2}EF\)\(\Leftrightarrow\dfrac{DE}{EF}=\dfrac{1}{2}\)
\(\Rightarrow k=\dfrac{2}{3}\)

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).

\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
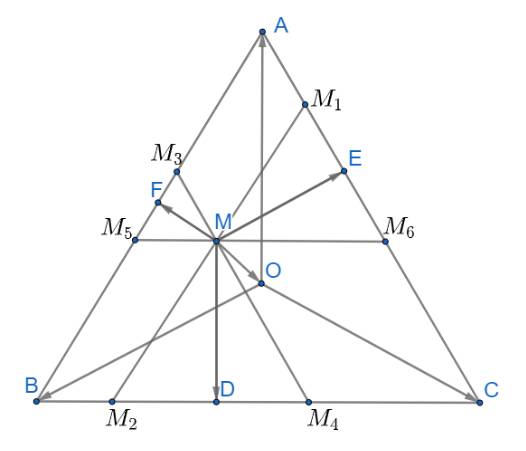

Qua M kẻ các đường thẳng song song với các cạnh của tam giác
A1B1 // AB; A2C2 // AC; B2C1 // BC.
Dễ thấy các tam giác MB1C2; MA1C1;MA2B2 đều là các tam giác đều. Ta lại có MD  B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
B1C2 nên MD cũng là trung điểm thuộc cạnh B1C2 của tam giác MB1C2
Ta có 2 =
= 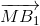 +
+ 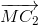
Tương tự: 2 =
= 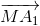 +
+ 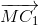
2 =
= 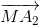 +
+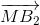
=> 2(  +
+ +
+ ) = (
) = (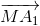 +
+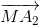 ) + (
) + (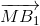 +
+ 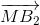 ) + (
) + (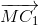 +
+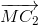 )
)
Tứ giác là hình bình hành nên
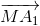 +
+ 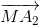 =
= 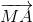
Tương tự: 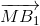 +
+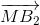 =
= 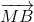
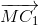 +
+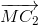 =
= 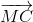
=> 2(  +
+ +
+ ) =
) = 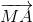 +
+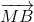 +
+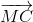
vì O là trọng tâm bất kì của tam giác và M là một điểm bất kì nên
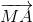 +
+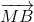 +
+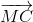 = 3
= 3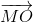 .
.
Cuối cùng ta có:
2(  +
+ +
+ ) = 3
) = 3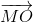 ;
;
=>  +
+ +
+ =
=