Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đoạn thẳng f: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [B, A] Đoạn thẳng i: Đoạn thẳng [C, A] Đoạn thẳng q: Đoạn thẳng [B, H] Đoạn thẳng r: Đoạn thẳng [D, E] Đoạn thẳng s: Đoạn thẳng [H, E] Đoạn thẳng t: Đoạn thẳng [F, G] Đoạn thẳng a: Đoạn thẳng [F, K] Đoạn thẳng b: Đoạn thẳng [A, F] Đoạn thẳng c: Đoạn thẳng [K, C] Đoạn thẳng d: Đoạn thẳng [H, K] Đoạn thẳng e: Đoạn thẳng [H, D] Đoạn thẳng f_1: Đoạn thẳng [K, D] Đoạn thẳng g_1: Đoạn thẳng [I, J] B = (-0.92, 2.22) B = (-0.92, 2.22) B = (-0.92, 2.22) C = (7.22, 2.18) C = (7.22, 2.18) C = (7.22, 2.18) Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm A: Điểm trên g Điểm D: Điểm trên f Điểm D: Điểm trên f Điểm D: Điểm trên f Điểm F: Giao điểm đường của j, k Điểm F: Giao điểm đường của j, k Điểm F: Giao điểm đường của j, k Điểm E: Giao điểm đường của j, h Điểm E: Giao điểm đường của j, h Điểm E: Giao điểm đường của j, h Điểm H: Giao điểm đường của l, m Điểm H: Giao điểm đường của l, m Điểm H: Giao điểm đường của l, m Điểm K: Giao điểm đường của n, p Điểm K: Giao điểm đường của n, p Điểm K: Giao điểm đường của n, p Điểm I: Giao điểm đường của h, e Điểm I: Giao điểm đường của h, e Điểm I: Giao điểm đường của h, e Điểm J: Giao điểm đường của i, f_1 Điểm J: Giao điểm đường của i, f_1 Điểm J: Giao điểm đường của i, f_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1
a) Ta thấy \(\widehat{BDI}=\widehat{BCA}\left(=\widehat{IBD}\right)\), suy ra ID // AJ
Tương tự DJ // IA. Vậy tứ giác AIDJ là hình bình hành hay AJ song song và bằng ID.
Từ đó suy ra AJ cũng song song và bằng HI hay AHIJ là hình bình hành. Vậy thì HA // IJ (1)
Xét tam giác HDK có IJ là đường trung bình nên HK // IJ (2)
Từ (1) và (2) suy ra H, A, K thẳng hàng.
b) Ta thấy do AHIJ là hình bình hành nên IJ = AH. Lại có \(IJ=\frac{HK}{2}\Rightarrow HA=\frac{HK}{2}\)
Vậy A là trung điểm của HK.
c) Do AIDJ là hình bình hành nên trung điểm IJ cũng là trung điểm AD.
Vậy khi D thay đổi, M luôn là trung điểm AD. Nói cách khác, khi M thay đổi M sẽ di chuyển trên đường trung bình ứng với đáy BC của tam giác ABC.

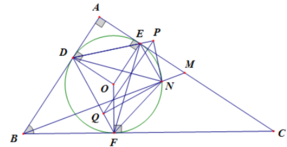
Vì DPN+DQN=90o+90o=180o nên DPNQ là tứ giác nội tiếp
=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)
Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN (6)
Từ (5) và (6) ta có FEN=QPN (7)
Tương tự ta có: EFN=PQN (8)
Từ (7) và (8) suy ra Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F
Theo quan hệ đường vuông góc – đường xiên, ta có
N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F
Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.
Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.
Câu hỏi của Hai Nguyen Lam - Toán lớp 9 - Học toán với OnlineMath Bạn tham khảo bài làm ở link này nhé!