Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tự kẻ hình :
a, tam giác ABC cân tại A (gt)
=> AB = AC (đn) (1)
góc ABC = góc ACB (đl)
góc ABC + góc ABM = 180 (kb)
góc ACB + góc ACN = 180 (kb)
=> góc ABM = góc ACN (2)
xét tam giác ABM và tam giác ACN có : BM = CN (gt) và (1); (2)
=> tam giác ABM = tam giác ACN (c-g-c)
=> MA = NA (đn)
=> tam giác AMN cân tại A (đn)
b, xét tam giác HBM và tam giác KCN có : MB = CN (gt)
góc M = góc N do tam giác AMN cân (câu a)
góc MHB = góc NKC = 90 do ...
=> tam giác HBM = tam giác KCN (ch - gn)
=> HB = CK (đn)
c, có AM = AN (Câu a)
AM = AH + HM
AN = AK + KN
HM = KN do tam giác HBM = tam giác KCN (câu b)
=> HM = KN

a) Tam giác ABC cân nên hai góc đáy bằng nhau : Góc ACB = Góc ABC
Ta lại có : Góc ABM = 180° - Góc ABC , Góc ACN = 180° - Góc ACB
Vậy Góc ABM = Góc ACN
Xét hai tam giác ABM và CAN , ta có :
AB = AC (gt)
Góc ABM = Góc ACN (cmt)
BM = CN (gt)
=> Tam giác ABM = tam giác CAN => AM = AN
Vậy tam giác AMN là tam giác cân tại A
b) Vì tam giác AMN cân => Góc AMB = Góc ANC
Xét tam giác MHB và tam giác CKN
Ta có : Góc MHB = Góc CKN ( Góc vuông )
Góc AMB = Góc ANC (cmt)
MB = CN (cmt)
=> tam giác MHB = tam giác NKC (g-c-g)
=> BH = CK
c) làm tương tự câu b
d) Tam giác ABM = Tam giác CKN => Góc HBM = Góc KCN
Góc CBO = Góc HBM và Góc KCN = Góc BCO ( đối đỉnh )
=> OBC là tam giác cân tại O
e) Khi BAC = 60° => Tam giác ABC đều
ta suy ra BM = AB => Tam giác ABM cân đỉnh B . Ta có Góc AMB = 1/2 ABC = 1/2 . 60 = 30°
Làm tương tự cho góc kia thì ANM = 30°
Góc  = 180 - 30° - 30° = 120°
Góc KCN = Góc BCO =60°
bn tham khảo!

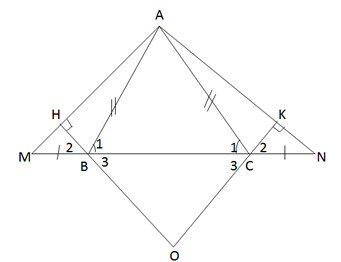
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800–12002=300M^=BAM^=1800–12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800–(ˆAMN+ˆANM)=1800–2.300=1200MAN^=1800–(AMN^+ANM^)=1800–2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).
mình cần lời giải gấp
A H M O B C N K
mình làm tắt nha
a,Tam giác ABC cân tại A => góc ABC= góc ACB
=> góc ABM = góc ACN
=> tam giác ABM = tam giác ACN (c.g.c)
=> AM=AN
=> tam giác AMN câc tại A
b,Tam giác AMN câc tại A => góc AMN = góc ANM
=> tam giác HMB = tam giác KNC (ch+gn)
=> BH=CK
c,Tam giác HBA = tam giác KCA (ch+cgv) => AH=AK
d,Ta có: tam giác HMB = tam giác KNC (phần c)
=> góc HBM = góc KCN
=> góc OBC = góc OCB (2 góc trên đối đỉnh vs OBC và OCB)
=> tam giác OBC cân tại O