Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M H K
a, xét tam giác BMH và tam giác CMK có : BM = MC do M là trđ của BC (Gt)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc BHM = góc CKM = 90
=> tam giác BMH = tam giác CMK (ch-gn)
b, tam giác BMH = tam giác CMK (câu a)
=> HM = MK (đn)
xét tam giác AMH và tam giác AMK có : AM chung
góc AHM = góc AKM = 90
=> tam giác AMH = tam giác AMK (ch-cgv)
c, tam giác ABC cân tại A (gt)
AM là trung tuyến
=> AM _|_ BC (định lí)

Lời giải:
a. Xét tam giác $MHB$ và $MKC$ có:
$\widehat{MHB}=\widehat{MKC}=90^0$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{MBH}=\widehat{MCK}$ (do $ABC$ cân tại $A$)
$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn)
b.
Xét tam giác $MHA$ và $MKA$ có:
$MA$ chung
$\widehat{MHA}=\widehat{MKA}=90^0$
$MH=MK$ (hệ quả từ $\triangle MHB=\triangle MKC$ phần a)
$\Rightarrow \triangle MHA=\triangle MKA$ (ch-cgv)

b/ Ta có: tam giác MHB = tam giác MKC
=> góc BHM = góc CKM = 900
=> CK vuông góc với AC
mà AB cũng vuông góc với AC
=> CK // AB (vì cùng vuông với AC) (1)
Mặt khác : HK vuông với AB
AC vuông với AB
=> HK // AC (2)
Từ (1) và (2) => tứ giác ACKH là hình bình hành => AC = HK (đpcm)
các pạn ai giải ra nhanh nhất ,lời giải hợp lí thì mk sẽ hậu tạ 3*

A B C M H K G I
a ) Xét tam giác MHB và tam giác MKC có :
BM = MC (gt)
Góc HMB = Góc CMK ( đối đỉnh )
MK = MH (gt)
=> tam giác MHB = tam giác MKC (c - g - c)
b ) Theo a ) tam giác MHB = tam giác MKC (c - g - c) => Góc BHM = Góc MKC ( Góc tương ứng )
Mà Góc BHM = 90 độ => Góc MKC = 90 độ
Tứ giác AHKC có Góc A + Góc H + Góc C + Góc K = 360 độ
<=> 3.90 + Góc C = 360 => Góc C = 90 độ
=> Tứ giác AHKC là hình chữ nhật => AC = HK
c ) đang nghĩ
C) theo kết quả câu a và b của đinh đức hùng ta được. AH=HB=KC. Từ đó suy ra H là trung điểm AB. CH là trung tuyến. AM cũng là trung tuyến => G là trọng tâm => BG là trung tuyến từ đỉnh B => I là trung điểm AC
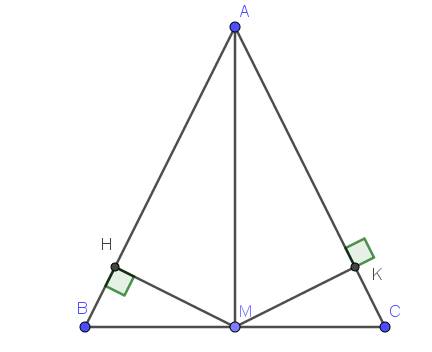
a, xét tam giác MBH và tam giác MCK ta có:
góc MHB= góc MKC=90 độ
BM=MC(gt)
góc B =góc C(gt)
vậy tam giác BMH = tam giác CMK(ch-gn)
b, xét tam giác AMH và tam giác AMK có:
AM chung
MH=MK( do tam giác BMH= tam giác CMK)
góc AHM= góc AKM=90 độ
suy ra tam giác AMH= tam giác AMK( ch-cgv)