Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\Delta ABC\)cân tại A
\(\Rightarrow AB=AC=12cm\)và \(\widehat{B}=\widehat{C}\)
Ta có: \(\Delta ABH\)vuông tại H
\(\Rightarrow\widehat{BAH}+\widehat{B}=90^o\)(1)
Ta lại có: \(\Delta ACH\)vuông tại H
\(\Rightarrow\widehat{CAH}+\widehat{C}=90^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{BAH}+\widehat{B}=\widehat{CAH}+\widehat{C}\)
mà \(\widehat{B}=\widehat{C}\)\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
Xét \(\Delta BAH\)và \(\Delta CAH\)ta có: +) \(\widehat{BAH}=\widehat{CAH}\)( cmt)
+) \(AB=AC\)
+) \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\Delta BAH=\Delta CAH\left(g.c.g\right)\)
\(\Rightarrow BH=HC\)( 2 cạnh tương ứng )
mà \(BC=10cm\)
\(\Rightarrow BH=HC=5cm\)
Ta có \(\Delta BAH\)vuông tại H nên theo định lý Py-ta-go ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2+5^2=12^2\)
\(\Rightarrow AH^2=12^2-5^2=144-25=119\)
\(\Rightarrow AH=\pm\sqrt{119}\)
mà \(AH>0\)\(\Rightarrow AH=\sqrt{119}\)
Vậy \(AH=\sqrt{119}\)

bài 1 : AH = \(\sqrt{119}\)cm
bài 2 : BN = \(\sqrt{49.54}\)cm
* hình tự vẽ
1/
Xét tam giác ABC: tam giác ABC là tam giác cân(gt) mà AH là đường cao(vì AH\(\perp\)BC)=> AH cũng là đường trung tuyến=> BH=HC
Ta có: BC=HB+HC, mà HB=HC(cmt)=> HB=HC=\(\frac{BC}{2}\)=> HB=HC= 5cm
Xét tam giác ACH, theo định lý Py ta go, có:
AH^2+ HC^2=AC^2
=> AH^2+ 5^2= 12^2
=> AH^2= 144-25
=> AH^2= 119=> AH= căn 119cm
2/ Xét tam giác BCA, theo định lý Py ta go, có:
BA^2+ AC^2= BC^2=> 12^2+5^2=BC^2
=> 144+25= BC^2=> BC^2= 169=>BC=13cm
Mà M là trung điểm BC(gt)=> MB=MC nên ta có BC=MB+MC=> MB=MC=\(\frac{BC}{2}\)=> MB=MC=6,5
Xét tam giác BMN, theo định lý Py ta go, có:
BN^2+NM^2= BM^2
=> BN^2+2,7^2=6,5^2=> BN^2 = 42,25-7,29=> BM^2= 34,96=> BM= căn 34,96cm

1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
2: Ta có: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=64\)
=>\(HA=\sqrt{64}=8\left(cm\right)\)
3: Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AH
4: Xét ΔAHM có
AE là đường trung tuyến
AE là đường cao
Do đó: ΔAHM cân tại A
=>AM=AH
Ta có: ΔAHN cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAN
=>\(\widehat{HAN}=2\cdot\widehat{HAC}\)
Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
=>\(\widehat{HAM}=2\cdot\widehat{HAB}\)
Ta có: AM=AH
AH=AN
Do đó: AM=AN
Ta có: \(\widehat{HAM}+\widehat{HAN}=\widehat{MAN}\)
=>\(\widehat{MAN}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{MAN}=2\cdot\widehat{BAC}\)
Để A là trung điểm của MN thì AM=AN và góc MAN=180 độ
=>góc MAN=180 độ
=>\(2\cdot\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=90^0\)

AC = AH + HC = 6 + 4 =10 ( cm )
Vì tam giác ABC cân tại A
=> AC = AB = 10 (cm)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
AB^2 = AH^2 + BH^2
=> BH^2 = AB^2 - AH^2
BH^2 = 10^2 - 6^2 = 100 - 36 = căn 64 = 8
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
BC^2 = HC^2 + HB^2
= 4^2 + 8^2 = 16 + 64 =căn 80
Vậy BC = căn 80
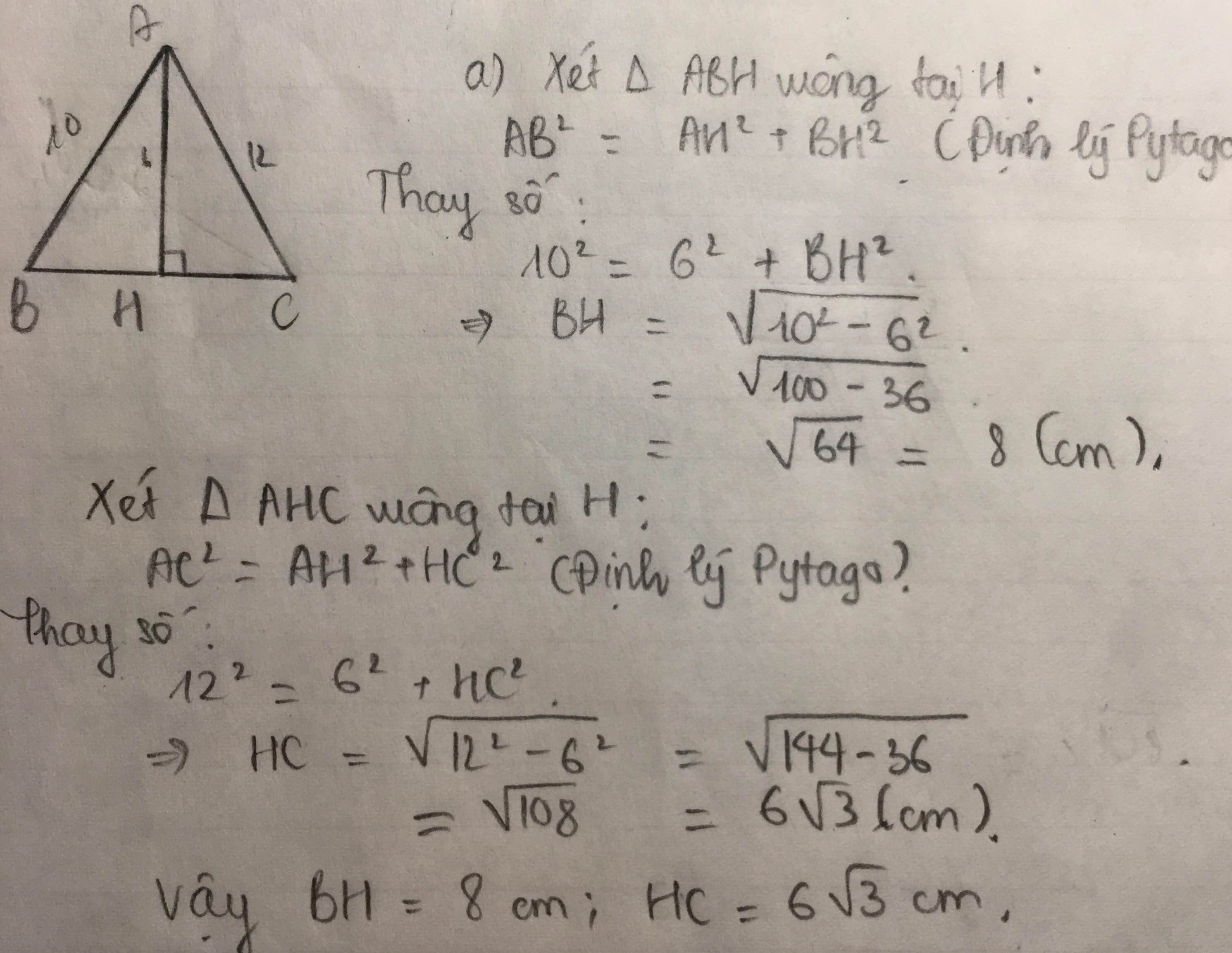
Vì AH vuông góc với BC mà tam giác ABC cân tại A (gt)
Nên AH vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow BH=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)
Áp dụng định lý Pi-ta-go vào tam giác ABH vuông tại H có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)
Hay \(AH^2=12^2-5^2\)
\(\Rightarrow AH^2=144-25\)
\(\Rightarrow AH^2=119\)
\(\Rightarrow AH=\sqrt{119}\)