
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


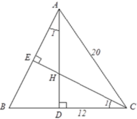
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm.
Đáp án: C

a. Lưu ý: Hai tam giác bằng nhau cũng là hai tam giác đồng dạng, với tỉ số đồng dạng là 1.
△ABD∼△ACD∼△AHE∼△BHD∼△BCE.
b. △ABC cân tại A mà AD là đường cao \(\Rightarrow\)AD cũng là trung tuyến
\(\Rightarrow\)D là trung điểm BC.
△ABD vuông tại D có:
\(AD^2+BD^2=AB^2\Rightarrow AD=\sqrt{AB^2-BD^2}=\sqrt{20^2-\left(\dfrac{24}{2}\right)^2}=16\left(cm\right)\)
△BHD∼△ABD \(\Rightarrow\dfrac{DH}{DB}=\dfrac{DB}{DA}\Rightarrow DH=\dfrac{BD^2}{AD}=\dfrac{\left(\dfrac{24}{2}\right)^2}{16}=9\left(cm\right)\)
\(AH=AD-DH=16-9=7\left(cm\right)\)
\(\dfrac{HB}{BA}=\dfrac{DB}{DA}\Rightarrow BH=\dfrac{AB.BD}{AD}=\dfrac{20.\dfrac{24}{2}}{16}=15\left(cm\right)\)
△ACD∼△AHE \(\Rightarrow\dfrac{CD}{HE}=\dfrac{AC}{AH}\Rightarrow HE=\dfrac{CD.AH}{AC}=\dfrac{\dfrac{24}{2}.7}{20}=4,2\left(cm\right)\)

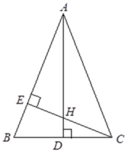
Kẻ đường cao AD. Xét ΔCBE và ΔABD có BEC=ADB=90 B E C ^ = A D B ^ = 90 ∘ và góc B chung nên ΔCBE ~ ΔABD (g.g) => B C A B = B E B D hay 24 A B = 9 12 => AB = 32cm.
Đáp án: B

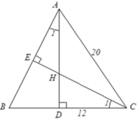
Tam giác ABC cân tại A nên B D = D C = B C 2 = 24 2 = 12 ( c m )
Theo định lý Py-ta-go, ta có A D 2 = A C 2 - D C 2 = 20 2 - 12 2 = 16 2
Nên AD = 16cm
Xét ΔCDH và ΔADB có:
C D H ^ = A D B ^ = 90 ∘
C 1 = A 1 (cùng phụ với B)
Do đó ΔCDH ~ ΔADB (g.g)
Nên H D B D = H C A B = C D A D , tức là H D 12 = H C 20 = 12 16 = 3 4
Suy ra HD = 9cm => AH = AD - HD = 16 - 9 = 7cm
Đáp án: B