Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)
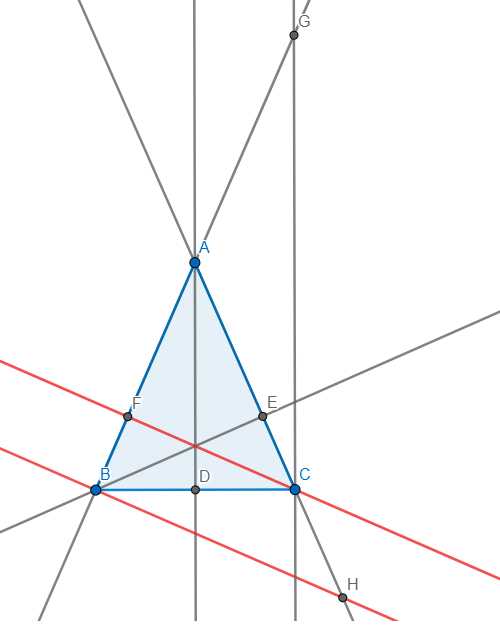

Gọi F là điểm đối xứng của CC qua AA
Ta được \(AF=AC=AB\)
\(A,F,C\)thẳng hàng
\(\Rightarrow\Delta BFC\perp B\)
Ta có: \(\Delta ABC\)cân tại A(gt)
\(AD\perp BC\left(gt\right)\)
\(\Rightarrow BD=DC\)
mà \(AF=AC\)
\(\Rightarrow AD\)//\(BF\)mà \(AD=\frac{BF}{2}\)(tính chất đường trung bình)
Áp dụng hệ thức lượng vào \(\Delta BFC\perp B\)đường cao BE ta được:
\(\frac{1}{BE^2}=\frac{1}{BF^2}+\frac{1}{BC^2}\)
\(\Leftrightarrow\frac{1}{BE^2}=\frac{1}{4AD^2}+\frac{1}{BC^2}\)
\(\Leftrightarrow\frac{1}{4k^2}=\frac{1}{4n^2}+\frac{1}{4m^2}\)
\(\Leftrightarrow\frac{1}{k^2}=\frac{1}{n^2}+\frac{1}{m^2}\left(đpcm\right)\)
#Shinobu Cừu

câu c nè: mik ns ý chính nhé
h bạn kẻ tiếp tuyến tại A
chứng minh đc AO vuông góc vs MN
=> OA vuông góc vs EF
do OA cố định
=> đường thẳng qua A vuông góc vs EF luôn đi qua 1 điểm cố định
do câu a va b bn làm đc rồi nên mik nghĩ bn cx hok giỏi rồi nên mik làm tắt nha

cho địa chỉ mail mình gửi bài giải cho latuanthiendhc@gmail.com
hix méo có ai làm đc à @@ hay là chỉ là cái lướt nhẹ qua = =