Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

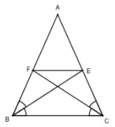
A B C E F
Ta có: \(\Delta ABC\) cân tại A (gt)
mà BE, CF lần lượt là tia phân giác của \(\widehat{ABC}\) và \(\widehat{ACB}\) (gt)
=> BE = CF
Xét \(\Delta ABE\) và \(\Delta ACF\) có:
BE = CF (cmt)
\(\widehat{ABE}=\widehat{ACF}\) \(\left(\widehat{ABC}=\widehat{ACB}=2\widehat{ABE}=2\widehat{ACF}\right)\)
AB = AC (\(\Delta ABC\) cân tại A)
Do đó: \(\Delta ABE=\Delta ACF\left(c.g.c\right)\)
=> AE = AF (2 cạnh tương ứng)
=> \(\Delta AFE\) cân tại A
mà \(\Delta ABC\) cân tại A
nên \(\widehat{ABC}=\widehat{AFE}\)
mà chúng ở vị trí đồng vị
=> FE // BC (dấu hiệu nhận biết)
=> BFEC là hình thang
mà BE = CF
=> BFEC là hình thang cân
Ta có: EF // BC (cmt)
=> \(\widehat{EFC}=\widehat{FCB}\) (2 góc so le trong)
mà \(\widehat{FCB}=\widehat{ECF}\) (CF là tia phân giác \(\widehat{ECB}\))
=> \(\Delta FEC\) cân tại E (t/c tam giác cân)
=> FE = EC (Đ/N tam giác cân)
mà hình thang BFEC cân
=> BFEC là hình thang cân có đáy nhỏ bằng cạnh bên

góc A là góc chung
AB=AC(giả thiết)
góc ABE= góc ACF(cmt)
=>tam giác ABE= tam giác ACF(c.g.c)
=>AE=AF
=>tam giác AEF cân tại A
=>AEF=180-A/2 (1)
có tam giác AEF cân tại A (gt) 180 độ nhé
=>góc ABC=180-A/2 (2)
từ (1) và (2) nên ^AFE=^ABC 2 góc đòng vị
=>FE song song với BC
mà ^B=^C
=>tứ giác BFEC là ht cân

+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
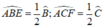
Mà tam giác ABC cân tại A nên ∠ B = ∠ C
Suy ra: ∠ ABE = ∠ ACF
Xét hai tam giác AEB và AFC
Có AB = AC ( ∆ ABC cân tại A)
∠ ABE = ∠ ACF (chứng minh trên)
∠ A là góc chung
⇒ ∆ AEB = ∆ AFC (g.c.g) ⇒ AE = AF ⇒ ∆ AEF cân tại A
⇒ ∠ AFE = ( 180 0 − ∠ A) / 2 và trong tam giác ∆ ABC: ∠ B = ( 180 0 − ∠A) / 2
⇒ ∠ AFE = ∠ B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: ∠ FEB = ∠ EBC (so le trong)
Lại có: ∠ FBE = ∠ EBC ( vì BE là tia phân giác của góc B)
⇒ ∠ FBE = ∠ FEB
⇒ ∆ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)

a) Xét \(\Delta ABE\) và \(\Delta ACF\) có :
AB = AC (\(\Delta ABC\)cân)
\(\widehat{A}\)chung
=> \(\Delta ABE\) = \(\Delta ACF\) (cạnh huyền - góc nhọn)
b) Có CF và BE là 2 đường cao
=> Giao điểm H là trực tâm
=> AH là đường cao của BC
c) Xét tứ giác BFEC , vì \(\Delta ABC\) cân
=> \(\widehat{ABC}=\widehat{ACB}\)
=> Tứ giác BFEC là hình thang cân vì 2 góc kề đáy bằng nhau .

Có: BE là tia pg của ^B(gt)
CF là tia og của C(gt)
Mà ^B=^C
=> ^ABE=^CBE=^ACF=^BCF
b) Xét ΔABE và ΔACF có:
^A : góc chung
AB=AC(gt)
^ABE=^ACF(cmt)
=>ΔABE=ΔACF(g..c.g)
=> AE=AF
=>ΔAEF cân tại A
=> \(\widehat{AFE\:}=\frac{180-\widehat{A}}{2}\) (1)
Có: ΔABC cân tại A(gt)
=> \(\widehat{ABC}=\frac{180-\widehat{A}}{2}\) (2)
Từ (1)(2) suy ra:
^AFE=^ABC. MÀ hai góc mày ở vị trí đồng vị
=>FE//BC
Mà ^B=^C(gt)
=> tứ giác BFEC là ht cân
nhanh v