Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \Delta AMBΔAMB và \Delta DMCΔDMC có:
AB=AC(gt)
AM=MD(gt)
MB=MC(gt)
=>\Delta AMB=\Delta DMC\left(c.c.c\right)ΔAMB=ΔDMC(c.c.c)
b) Vì: \Delta AMB=\Delta DMC\left(cmt\right)ΔAMB=ΔDMC(cmt)
=> \widehat{MAB}=\widehat{MDC}MAB=MDC . Mà hai góc này ở vị trí sole trong
=>AB//DC
# Study well 'v'
a) Xét \(\Delta AMB\) và \(\Delta DMC\) , ta có:
AB = AC (gt)
AM=MD (gt)
MD=MC (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.c.c\right)\)
b) Vì: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB=\widehat{MDC}}\)
\(\Rightarrow AB\) // \(DC\)
#Chúc bạn học tốt ^^

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M la trung điểm của AC
M là trung điểm của BD
DO đó: ABCD là hình bình hành
Suy ra: AB//CD và AB=CD

a) xét tam giác AMBvà tam giácCMD có
góc AMB=gócCMD(đối đỉnh)
MA=MC
MD=MB
suy ra tam giác AMB=tam giác CMD
b) tam giác AMB=tam giác CMD(câu a)
AB=CD(hai cạnh tương ứng)
góc DCM=góc MAB(hai góc tương ứng và so le trong)
suy ra AB//CD
câu c đang tìm hiểu từ từ nha tick đi rồi giải câu c luôn cho
A B E D C M
a) Xét \(\Delta\)AMB & \(\Delta\)CMD có:
MB=MD( giả thiết)
góc AMB= góc CMD(2 góc đối đỉnh)
AM=MC( vì M là trung điểm của AC)
=>\(\Delta\)AMB=\(\Delta\)CMD(c.g.c)
b) Theo a) \(\Delta\)AMB=\(\Delta\)CMD
=>AB=CD(2 cạnh tương ứng)
=>góc BAM= góc DCM( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong=>AB//CD
c) theo b) AB//CD
=> góc ABC= góc BCE( 2 góc so le trong)
Ta có: AB=CD( theo c/m b)
mà CD=CE( vì C là trung điểm DE)
=>AB=EC
Xét \(\Delta\)ABC & \(\Delta\)ECB có:
AB=EC( theo c/m trên)
góc ABC= góc ECB( theo cm trên)
AC là cạnh chung
=>\(\Delta\)ABC=\(\Delta\)ECB(c.g.c)
=>góc ACB= góc EBC( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=>AC//BE

a/(c.g.c)
b/ CE=AB ( cặp cạnh tương ứng)
Mà: AB<BC( cạnh huyền lớn nhất)
Nên CE<BC
c/góc ABM=góc CEM(cặp góc tương ứng) (1)
Xét tam giác BCE có: CE<BC( CMT)
Suy ra góc CEM<góc MBC (2) ( Quan hệ giữa góc và cạnh đối diện trong 1 tam giác)
Vậy: từ (1) và (2), ta có: góc ABM< góc MBC
d/góc ABM=góc CEM, lại ở vị trí SLT nên AE//BC

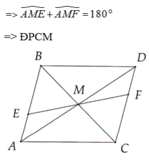
1) Chứng minh ΔAMB=ΔCMD
Xét ΔAMB và ΔCMD có
BM=MD(gt)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
AM=MC(do M là trung điểm của AC)
Do đó: ΔAMB=ΔCMD(c-g-c)
2) Chứng minh AB=CD và AB//CD
Ta có: ΔAMB=ΔCMD(cmt)
⇒AB=CD(hai cạnh tương ứng)
Ta có: ΔAMB=ΔCMD(cmt)
⇒\(\widehat{BAM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{BAM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)(đpcm)
3) Chứng minh E,M,F thẳng hàng
Xét tứ giác AFCE có
AE//FC(AB//CD, E∈AB, F∈CD)
AE=FC(gt)
Do đó: AFCE là hình bình hành(dấu hiệu nhận biết hình bình hành)
⇒hai đường chéo AC và FE cắt nhau tại trung điểm của mỗi đường(định lí hình bình hành)
mà M là trung điểm của AC(gt)
nên M là trung điểm của FE
hay F,M,E thẳng hàng(đpcm)