Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
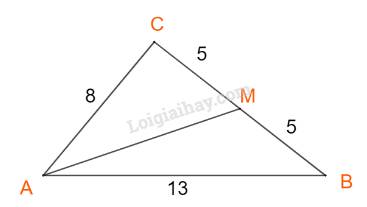
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)

Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)

a: \(\left\{{}\begin{matrix}x_G=\dfrac{2+4+2}{3}=\dfrac{8}{3}\\y_G=\dfrac{1+0+3}{3}=\dfrac{4}{3}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_I=\dfrac{2+4}{2}=3\\y_I=\dfrac{1+0}{2}=\dfrac{1}{2}\end{matrix}\right.\)

Đặt \(m=2018,\frac{\sin B+m\sin C}{m\cos B+\cos C}=\sin A\Leftrightarrow b+mc=a\left(m\cos B+\cos C\right)\)
\(\Leftrightarrow b+mc=\frac{m\left(a^2+c^2-b^2\right)}{2c}+\frac{a^2+b^2-c^2}{2b}\)
\(\Leftrightarrow2bc\left(b+mc\right)=mb\left(a^2+c^2-b^2\right)+c\left(a^2+b^2-c^2\right)\)
\(\Leftrightarrow2b^2c+2mbc^2=mba^2+mbc^2-mb^3+ca^2+cb^2-c^3\)
\(\Leftrightarrow\left(c+mb\right)\left(b^2+c^2-a^2\right)=0\Leftrightarrow a^2=b^2+c^2\)
Vậy tam giác ABC vuông tại A
Dễ dàng CM được \(S_{ABC}=6.S_{MBG}\Rightarrow bc=12.S_{MBG}\).Do vậy ta cần CM bc chia hết cho 12
( ta sử dụng tính chất của số chính phương)
- Số chính phương chia 3 chỉ dư 0 hoặc 1
- Số chính phương chia 4 chỉ dư 0 hoặc 1
- Số chính phương lẻ chia 8 chỉ dư 1
*) Ta thấy trong 2 số \(b^2,c^2\)có ít nhất 1 số chia hết cho 3. giả sử không có số nào trong 2 số đó chia hết cho 3. Khi đó mỗi số đều chia 3 dư 1. Do đó a2 chia 3 dư 2 ( trái với tính chất số chính phương)
Do 3 là số nguyên tố nên trong 2 số b,c có ít nhất 1 số chia hết cho 3 . (1)
*)Chứng minh trong 2 số b,c có ít nhất 1 số chia hết cho 4. giả sử không có số nào trong 2 số đó chia hết cho 4. Khi đó \(b=4m+r;c=4n+q;r,q\in\left\{1;2;-1\right\}\)
+ Nếu \(r,q\in\left\{1;-1\right\}\Rightarrow a^2\)chia 4 dư 2 ( vô lý)
+ Nếu \(r\in\left\{-1;1\right\},q=2\) hoặc ngược lại thì a2 là số lẻ và a2 chia 8 dư 5 ( vô lý)
+ Nếu r=q=2 thì \(a^2=4\left(2m+1\right)^2+4\left(2n+1\right)^2\Rightarrow\)a chẵn
Đặt \(a=2p\Rightarrow p^2=\left(2m+1\right)^2+\left(2n+1\right)^2\Rightarrow p^2\)chia 4 dư 2 ( vô lý)
Vậy trong 2 số b,c có ít nhất 1 số chia hết cho 4 (2)
Từ (1) và (2) => đpcm

1) R=3
\(\left\{{}\begin{matrix}\widehat{A}=30^o\\\widehat{B}=45^o\end{matrix}\right.\rightarrow\widehat{C}=105^o\)
Theo đl sin ta có : \(\frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}=2R\)\(\Leftrightarrow\frac{BC}{sin30^o}=\frac{AC}{sin45^o}=\frac{AB}{sin105^o}=2.3=6\)
=> \(\left\{{}\begin{matrix}BC=3\\AC=4,2\\AB=5,8\end{matrix}\right.\)
Độ dài đường trung tuyến từ A là :
\(m_a=\sqrt{\frac{2\left(AC^2+AB^2\right)-BC^2}{4}}\approx4,8\)
\(S=\frac{AB.AC.BC}{4R}=\frac{5,8.4,2.3}{4}=6,09\)
\(p=\frac{AB+AC+BC}{2}=6,5\)
Ta có : S = pr => Bán kính đường tròn nội tiếp tam giác là: \(r=\frac{S}{p}=\frac{6,09}{6,5}\approx1\)
2) A B C M
AB=3; BC =8; \(cos\widehat{AMB}=\frac{5\sqrt{13}}{26}\)
M là trung điểm BC => BM=CM = 4
Áp dụng hệ quả của đl cosin trong tam giác AMB có :
\(cos\widehat{AMB}=\frac{BM^2+AM^2-AB^2}{2.BM.AM}=\frac{4^2+AM^2-3^2}{2.4.AM}=\frac{5\sqrt{13}}{26}\)
=> AM = 3,6
Lại có : \(AM=\sqrt{\frac{2.\left(AC^2+AB^2\right)-BC^2}{4}}=\sqrt{\frac{2\left(AC^2+3^2\right)-8^2}{4}}=3,6\)
=> AC = 7
Trong tam giác góc lớn hơn thì đối diện với cạnh lớn hơn và ngược lại
=> A là góc lớn nhất
\(cosA=\frac{AC^2+AB^2-BC^2}{2.AC.AB}=\frac{7^2+3^3-8^2}{2.7.3}=\frac{-1}{7}\)
\(\Rightarrow\widehat{A}\approx98^o\)

a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc.\cos A\\ \Leftrightarrow {a^2} = {8^2} + {5^2} - 2.8.5.\cos {120^ \circ } = 129\\ \Rightarrow a = \sqrt {129} \end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{\sqrt {129} }}{{\sin {{120}^ \circ }}} = \frac{8}{{\sin B}} = \frac{5}{{\sin C}}\\ \Rightarrow \left\{ \begin{array}{l}\sin B = \frac{{8.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,61\\\sin C = \frac{{5.\sin {{120}^ \circ }}}{{\sqrt {129} }} \approx 0,38\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat B \approx 37,{59^ \circ }\\\widehat C \approx 22,{41^ \circ }\end{array} \right.\end{array}\)
b) Diện tích tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.8.5.\sin {120^ \circ } = 10\sqrt 3 \)
c)
+) Theo định lí sin, ta có: \(R = \frac{a}{{2\sin A}} = \frac{{\sqrt {129} }}{{2\sin {{120}^ \circ }}} = \sqrt {43} \)
+) Đường cao AH của tam giác bằng: \(AH = \frac{{2S}}{a} = \frac{{2.10\sqrt 3 }}{{\sqrt {129} }} = \frac{{20\sqrt {43} }}{{43}}\)

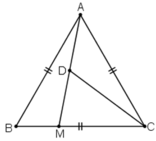
a) Do tam giác ABC là tam giác đều nên 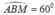 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
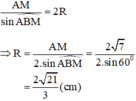
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có: