Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) XétΔABC vg tại A
⇒ BC²=AB²+AC²
⇒ BC=17cm
Xét ΔABH và ΔCBA có:
góc AHB= góc CBA
góc B: chung
⇒ ΔABH ∞ ΔCBA (g.g)
⇒ AB/BC=BH/BA
⇒ BH=AB²/BC
⇒ BH=64/17
Xét ΔABH vg tại H
⇒AB²=BH²+AH²
⇒ AH=120/17
b) xét tg AMHN có: góc AMH= góc ANH= góc MAN=90
⇒ tg AMHN là hcn (dhnb)
⇒ AH=MN (t/c hcn)
⇒ MN=120/17
, Ta thấy tam giác AMH đồng dạng tam giác AHB (g.g) suy ra AM/AH = AH/ AB => AM.AB =AH^2
tam giác ANH đồng dạng tam giác AHC (g.g)
=> AN/AH = AH/AC
=> AN.AC = AH^2
suy ra AM.AB = AN.AC.

áp dụng Pytago cho tam giác ABC ta đc: BC= \(\sqrt{15^2+8^2}=17\)
diện tích tam giác ABC=1/2. AB.BC = 1/2 AH.BC => AB.BC=AH.BC=> AH=15.8:17=120/17
b, Tứ giác AMNH là hình chữ nhật vì có 3 góc vuông.
suy ra MN=AH = 120/17
c, Ta thấy tam giác AMH đồng dạng tam giác AHB (g.g) suy ra AM/AH = AH/ AB => AM.AB =AH^2
tam giác ANH đồng dạng tam giác AHC (g.g) => AN/AH = AH/AC => AN.AC = AH^2
suy ra AM.AB = AN.AC.
d. góc HAB = góc ACB ( cùng phụ góc CAH)
suy ra tam giác AMH đồng dạng tam giác CAB.
theo bài ta có \(S_{AMHN}=2S_{AMH}=\frac{1}{2}S_{CAB}\)
suy ra \(\frac{S_{AMH}}{S_{CAB}}=\frac{1}{4}\) mà 2 tam giác này đồng dạng nên suy ra \(\left(\frac{AH}{BC}\right)^2=\frac{1}{4}\Rightarrow\frac{AH}{BC}=\frac{1}{2}\Rightarrow AH=\frac{1}{2}BC\)
do đó tam giác ABC phải vuông cân.

mình tóm tắt thôi nha
▲MHA đồng dạng ▲HBA(g-g)
▲ABC đồng dạng ▲HBA(g-g)
suy ra ▲MHA đồng dạng ▲ABC
▲MHA đồng đăng ▲ANM
suy ra ▲ANM đồng dạng ▲ABC
suy ra tỉ số rồi ra
b)áp dụng PY-ta-go thì
BC =25cm
ta có S▲ABC =1/2 AB.AC
mặt khác S▲ABC=1/2 AH.BC
suy ra AB.AC=AH.BC
suy ra AH=(15.20)/25=12cm
ta có ▲ANM đồng dạng ▲ABC
suy ra \(\frac{NM}{BC}=\frac{AM}{AC}\)
\(\Rightarrow\frac{AH}{BC}=\frac{AM}{AC}=\frac{12}{25}\)
\(\Rightarrow\frac{S▲ANM}{S▲ABC}=\left(\frac{12}{25}\right)^2=0,2304\)
nhớ kick cho mình nha
câu b) tính tỉ số diện tích dùm mình lun nha bạn cần gắp lắm!!!!!!!!!!

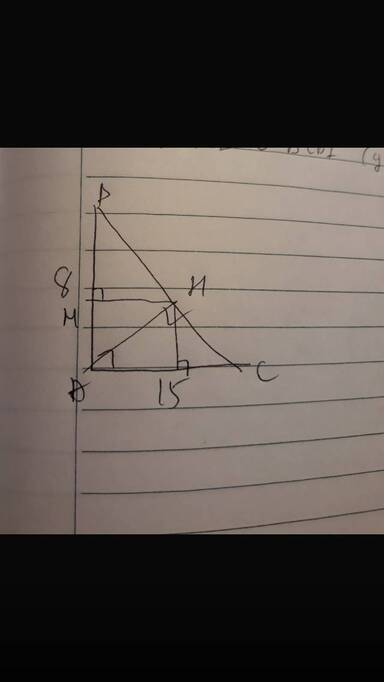
B H M A C N
( Hình ảnh chỉ mang tính chất minh họa )
a) Tính BC và AH :
Tam giác ABC vuông tại A, áp dụng định lý Pytago vào tam giác ABC :
AB2+AC2=BC2AB2+AC2=BC2
82+152=BC282+152=BC2
⇒BC=17(cm)⇒BC=17(cm)
Ta có : SABC=12⋅AB⋅AC=12⋅AH⋅BCSABC=12⋅AB⋅AC=12⋅AH⋅BC
⇔AH=AB⋅ACBC=8⋅1517=12017(cm)⇔AH=AB⋅ACBC=8⋅1517=12017(cm)
b) Có Aˆ=900A^=900(giả thiết), Mˆ=900M^=900(hình chiếu), Nˆ=900N^=900(hình chiếu)
=> Tứ giác AMHN là hình chữ nhật (tứ giác có 3 góc bằng 90 độ).
Vì tứ giác AMHN là hình chữ nhật => Hai đường chéo bằng nhau.
⇒MN=AH=12017(cm)⇒MN=AH=12017(cm)
c) Vì N là hình chiếu của H trên AC ⇒N∈AC⇒N∈AC
mà MHMH//AN(hcn)AN(hcn) => MHMH//ACAC
Theo hệ quả của định lý Ta-let => AMAB=ANACAMAB=ANAC
Suy ra : AM⋅AC=AN⋅AB(đpcm)