Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có 
Do đó, y'<0 <=> 
<=> x≠1 và x2 -2x -3 <0
<=> x≠ 1 và -1<x<3 <=> x∈ (-1;1) ∪ (1;3).
b) Ta có 
Do đó, y’≥0 <=> 
<=> x≠ -1 và x2 +2x -3 ≥ 0 <=> x≠ -1 và x ≥ 1 hoặc x ≤ -3 <=> x ≥ 1 hoặc x ≤ -3
<=> x∈ (-∞;-3] ∪ [1;+∞).
c).Ta có 
Do đó, y’>0 <=>
<=> -2x2 +2x +9>0 <=> 2x2 -2x -9 <0 <=> 
<=> x∈ 
vì x2 +x +4 = (x+1/2)2 + 15/4 >0, với ∀ x ∈ R.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) C = (-4.78, -5.6) C = (-4.78, -5.6) C = (-4.78, -5.6) D = (7.82, -7.32) D = (7.82, -7.32) D = (7.82, -7.32) E = (-4.82, -6.92) E = (-4.82, -6.92) E = (-4.82, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) G = (-7.14, -8.07) G = (-7.14, -8.07) G = (-7.14, -8.07) H = (12.33, -8.07) H = (12.33, -8.07) H = (12.33, -8.07) I = (-1.74, -9.56) I = (-1.74, -9.56) I = (-1.74, -9.56) J = (18.64, -9.56) J = (18.64, -9.56) J = (18.64, -9.56) K = (-7.17, -8.04) K = (-7.17, -8.04) K = (-7.17, -8.04) L = (12.3, -8.04) L = (12.3, -8.04) L = (12.3, -8.04) M = (-7.24, -7.99) M = (-7.24, -7.99) M = (-7.24, -7.99) N = (12.23, -7.99) N = (12.23, -7.99) N = (12.23, -7.99)
1/ \(y=x^{-1}+\frac{2}{3}x^{-2}-\frac{2}{3}\Rightarrow y'=-\frac{1}{x^2}-\frac{4}{3x^3}\)
\(3x^3y'+3x+4=3x^3\left(-\frac{1}{x^2}-\frac{4}{3x^3}\right)+3x+4\)
\(=-3x-4+3x+4=0\) (đpcm)
2/ \(y'\le0\)
\(\Leftrightarrow3x^2-10x+7\le0\)
\(\Leftrightarrow1\le x\le\frac{7}{3}\)
a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
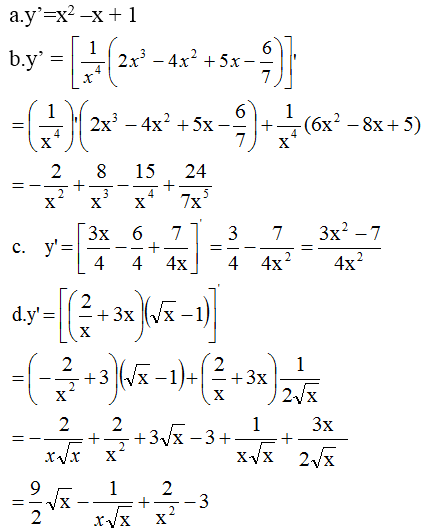
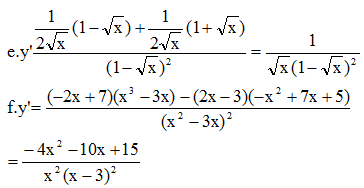
\(y'=x^2-6x\)
y' > 0 =>x<0;6<x
y' <3=>\(3-2\sqrt{3}< x< 3+2\sqrt{3}\)
\(y'\left(x\right)=3x^2-6x\).
a) \(y'\left(x\right)>0\)\(\Leftrightarrow3x^2-6x>0\)\(\Leftrightarrow\left[{}\begin{matrix}x< 0\\x>2\end{matrix}\right.\).
Vậy \(x< 0\) hoặc \(x>2\) thì \(y'\left(x\right)>0\).
b) \(y'\left(x\right)< 3\)\(\Leftrightarrow3x^2-6x< 3\)\(\Leftrightarrow3x^2-6x-3< 0\)\(\Leftrightarrow1-\sqrt{2}< x< 1+\sqrt{2}\).
Vậy \(1-\sqrt{2}< x< 1+\sqrt{2}\) thì \(y'\left(x\right)< 3\).