Question

[Truy kích]

Cho \(p\left(x\right)=Ax^3+Bx^2+Cx+D\ge0\). Tại sao với \(A< 0\) thì tồn tại \(x\in R\) thỏa mãn \(p(x)\ge 0\) và hiển nhiên tồn tại \(x\) thỏa mãn \(p(x)<0 \forall x\in R\)

->KLuận: phải tồn tại ít nhất một nghiệm dương

Ai giải thích giúp e với !

Answer 1

[Nguyễn Việt Lâm]

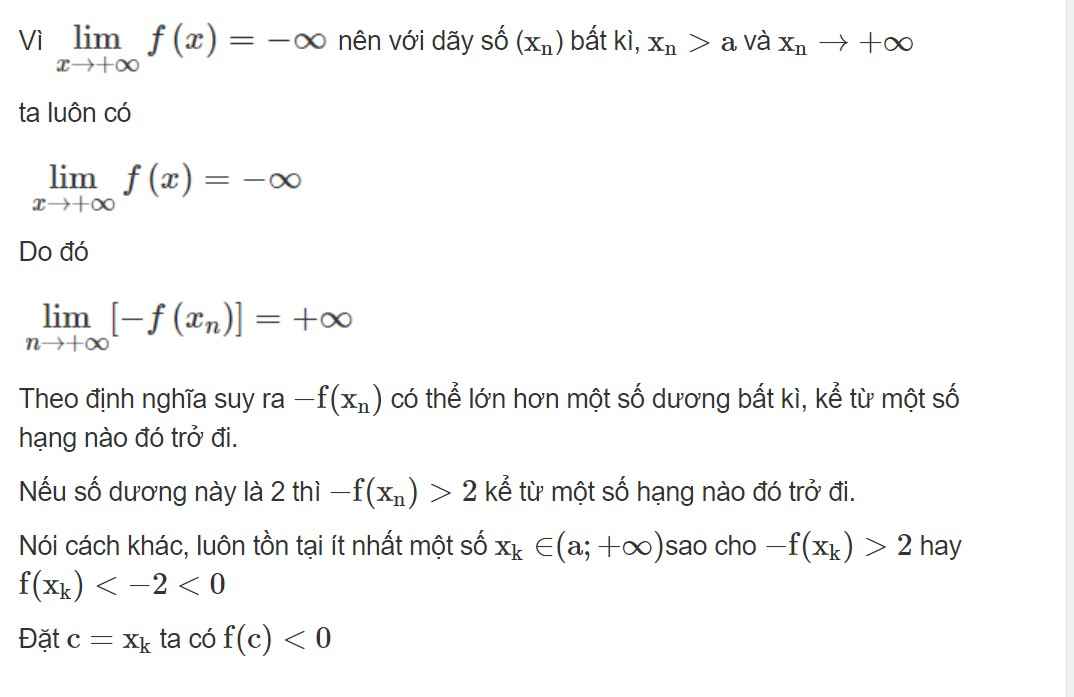
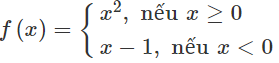
À cái kết luận đó liên quan tới lý thuyết đồ thị của các hàm bậc 3 mà lên lớp 12 mới học nên bạn thấy hơi lạ là đúng rồi :(

Bạn cứ hiểu hàm bậc 3 p(x) là một hàm mà miền giá trị của nó luôn chạy từ \(\left(-\infty;+\infty\right)\) bất chấp các hệ số A, B, C, D bằng bao nhiêu, do đó luôn chọn được 1 giá trị x nào đó sao p(x) nằm trên miền dương.

Đồng thời khi A<0 thì ta có \(\lim\limits_{x\rightarrow+\infty}p\left(x\right)=-\infty\) nên luôn tồn tại 1 giá trị x đủ lớn làm cho p(x) âm.

Hay bạn cứ nghĩ đơn giản cho A, B, C, D các giá trị bất kì trong đó A<0, rồi cho x một giá trị lớn cỡ vài tỉ thì kiểu gì p(x) cũng âm

Answer 2

[Nguyễn Việt Lâm]

Bạn cần ghi đầy đủ bài toán, ghi thiếu thế này thì chịu thua thôi bạn ạ